shine's dev log
[알고리즘] Activity Selection (Greedy Algorithm 활용) 본문
1. Activity Selection 코드
def activity_selection(S, F, k, n, result):
m = k + 1
while m <= n and S[m] < F[k]:
m = m + 1
if m <= n:
result.append('A' + str(m + 1))
return activity_selection(S, F, m, n, result)
else:
return None
result = ['A1']
S = [1, 2, 4, 1, 5, 8, 9, 11, 13]
F = [3, 5, 7, 8, 9, 10, 11, 14, 16]
# Initial call
activity_selection(S, F, 0, len(S)-1, result)
print(result)
위의 코드는 Activity Selection 문제를 Greedy Algorithm으로 수행하는 python 코드다.
2. 기본 알고리즘
Activity Selection은 다양한 Activity의 시작시각과 끝시각이 있을 경우, 가장 많은 Activity를 할 수 있는 Activity 집합을 고르는 알고리즘이다.
Activity Selection을 Greedy Algorithm 방식으로 푸는 원리는 다음과 같다.
무조건 남는 resource(시간)이 가장 크도록 선택 = 가장 빨리 끝나는 activity 선택
즉 한마디로 현재 남은 시간 중에서 무조건 가장 빨리 끝나는 activity를 선택하면 되는 것이다.
아래 예시를 통해 자세히 알아보자.

위의 표는 Activity 9개의 시작시각과 끝시각을 나타낸 표이다. 각 Activity를 타임라인에 나타내보면 아래 그림과 같다.
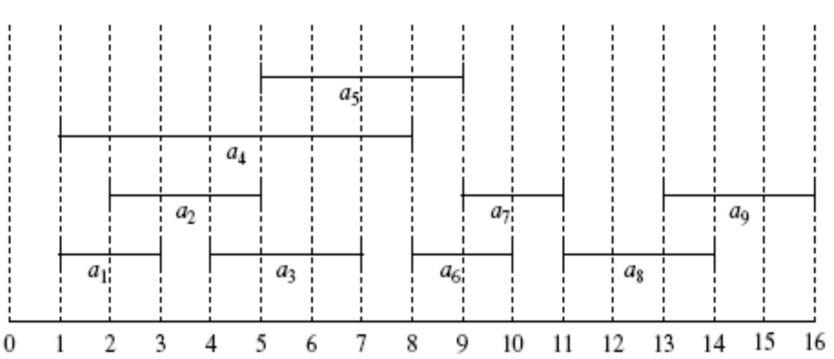
그럼 이제 앞서 살펴본 하나의 원칙 "남은 시간 중에서 가장 빨리 끝나는 Activity를 선택하라" 를 적용해 Activity selection 알고리즘을 풀어보겠다.
1) 우선 초기조건은 남은 시간은 0~16이다. 이 중 가장 빨리 끝나는 Activity는 a1이다. -> a1 선택
2) a1을 선택하고 난 뒤 남은 시간은 3~16이다. 이 중 가장 빨리 끝나는 Activity는 a3이다. -> a3 선택
3) a3을 선택하고 난 뒤 남은 시간은 7~16이다. 이 중 가장 빨리 끝나는 Activity는 a6이다. -> a6 선택
4) a6을 선택하고 난 뒤 남은 시간은 10~16이다. 이 중 가장 빨리 끝나는 Activity는 a8이다. -> a8 선택
5) a8을 선택하고 난 뒤 남은 시간은 14~16이다. 이 중 선택할 수 있는 Activity는 없다. -> 종료
즉 위와 같은 과정을 통해 나온 결론은 a1, a3, a6, a8이다.
다시 코드로 돌아가보자.
def activity_selection(S, F, k, n, result):
m = k + 1
while m <= n and S[m] < F[k]:
m = m + 1
if m <= n:
result.append('A' + str(m + 1))
return activity_selection(S, F, m, n, result)
else:
return None
Activity Selection의 핵심은 남은 시간 중 가장 빨리 끝나는 activity를 찾는 것이다.
위의 코드에서 초기의 k값은 남은 시간의 시작점을 명시한다. 이후 m과 k index를 통해 남은 시간 중 가장 빨리 끝나는 activity를 'S[m] < F[k]' 부등식을 통해 찾게 된다.
이렇게 찾은 activity를 result 리스트에 붙여넣는다.
찾은 activity가 끝나는 시각인 m 값을, 다음 activity_selection 함수에서 남은 시간의 시작점을 나타내도록 parameter로 넘겨주면 알고리즘이 완성된다.
result = ['A1']
S = [1, 2, 4, 1, 5, 8, 9, 11, 13]
F = [3, 5, 7, 8, 9, 10, 11, 14, 16]
# Initial call
activity_selection(S, F, 0, len(S)-1, result)
print(result)
코드에서 S, F 즉 activity가 시작하고 끝나는 시각을 나타낸 리스트를 선언하는 부분에 한가지 특징이 있다.
result 결과값에 이미 'Activity 1'이 들어있는 것이다.
이는 우리가 이미 Activity를 끝나는 시각을 기준으로 정렬했기 때문에, Activity1은 무조건 포함되기 때문에 미리 결과에 집어넣은 것이다.
3. 시간복잡도
Activity Selection의 시간복잡도의 경우, n 이다.
worst case의 경우, 모든 activity를 확인하는 경우인데, 이 경우, O(n)이 된다.
하지만, 이것은 끝나는 시각이 이미 정렬되어있다고 가정한 경우이기 때문에, 만약 끝나는 시각이 정렬되어있지 않다면 추가적으로 sort 하는데 걸리는 시간복잡도가 추가된다.
위 내용은 공부하며 작성한 것으로, 오류가 있을 수 있습니다.
'프로그래밍, 알고리즘' 카테고리의 다른 글
| [알고리즘] The Longest Common Subsequence(LCS) (Dynamic Programming 활용) (1) | 2021.10.30 |
|---|---|
| [알고리즘] Quick Sort 의 개념 (0) | 2021.10.26 |
| [알고리즘] Maximum-subarray 구하기 (Divide-and-conquer 활용) (0) | 2021.10.23 |
| [알고리즘] Merge sort (Divide-and-conquer 활용) (0) | 2021.10.03 |
| [알고리즘] Insertion sort 란? (0) | 2021.09.24 |




