shine's dev log
[알고리즘] The Longest Common Subsequence(LCS) (Dynamic Programming 활용) 본문
[알고리즘] The Longest Common Subsequence(LCS) (Dynamic Programming 활용)
dong1 2021. 10. 30. 23:151. LCS 코드
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1)
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n))
X = ['h', 'e', 'r', 'o', 'i', 'c', 'a', 'l', 'l', 'y']
Y = ['s', 'c', 'h', 'o', 'l', 'a', 'r', 'l', 'y']
print(lcs(X, Y, len(X), len(Y)))
위의 코드는 LCS를 recursive 하게 수행하는 python 코드다. (Dynamic Programming 방식 아님)
def LCS_dp(X, Y, m, n):
table = []
for i in range(0, m+1):
line = []
for j in range(0, n+1):
line.append(0)
table.append(line)
for i in range(0, m):
for j in range(0, n):
if X[i] == Y[j]:
table[i][j] = table[i-1][j-1] + 1
elif table[i-1][j] >= table[i][j-1]:
table[i][j] = table[i-1][j]
else:
table[i][j] = table[i][j-1]
return table
X = ["A", "B", "C", "D", "E", "F"]
Y = ["G", "B", "C", "D", "F", "E"]
result = LCS_dp(X, Y, len(X), len(Y))
print(result)
위의 코드는 LCS를 Dynamic Programming 방식으로 수행하는 python 코드다.
2. 기본 알고리즘
LCS는 두개의 배열에 공통으로 존재하는 최대 길이의 sub-array를 구하는 알고리즘이다. 꼭 연속적일 필요는 없으나, 순서는 맞아야 한다는 특징이 있다.
예를 들어 "heroically"라는 배열과 "scholarly" 라는 배열이 있을 경우, 아래 그림과 같이 "holly" 라는 sub-array가 LCS가 되며, 5개의 원소로 이루어져있으므로, 결과값은 5가 나온다.
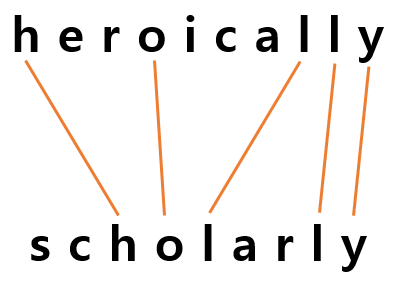
LCS를 해결 하는 기본적인 아이디어는 다음과 같다.
LCS를 구하려는 2개의 배열 X, Y와 이 두 배열의 LCS를 나타내는 Z 라는 sub-array가 있다고 하자.
(위의 예시에서는 X는 "heroically" Y는 "scholarly" Z는 "holly"가 된다.)
이제 총 2가지 케이스로 나눌 수 있는데,
Case 1) X와 Y의 가장 마지막 원소가 같은 경우
- 이 경우에는 자동으로 X, Y의 마지막 원소가 Z의 가장 마지막 원소가 된다.
- 따라서 LCS에 1을 추가하고, X, Y의 가장 마지막 원소를 제외한 나머지 배열들을 가지고 LCS를 다시 구하면 된다.

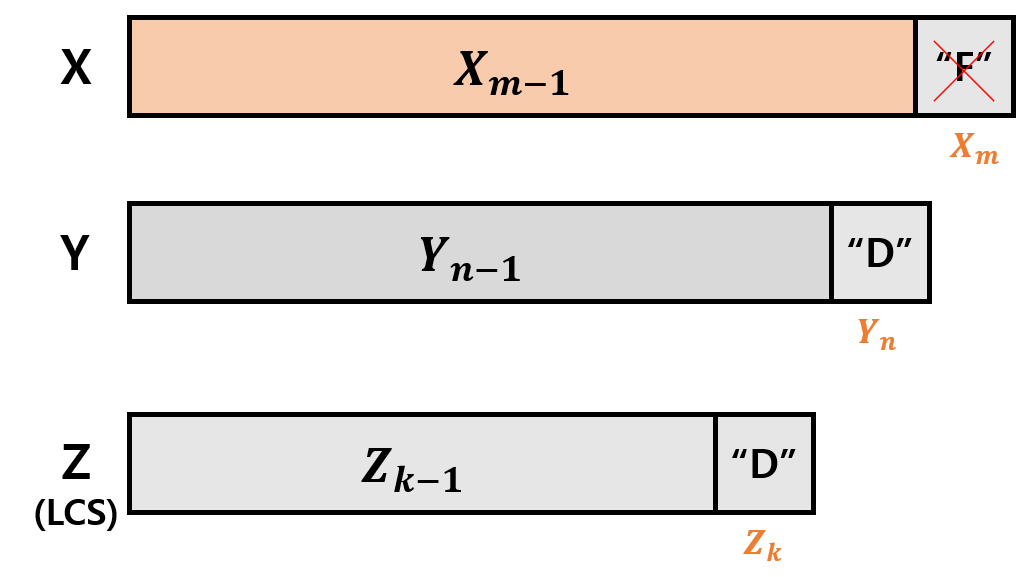
Case 2) X와 Y의 가장 마지막 원소가 다른 경우
- 이 경우 두가지 케이스가 나온다.
- case 2-1) 은 Y의 마지막 원소가 Z의 마지막 원소와 같은 경우이다. 이 경우, X의 마지막 원소를 없애고 다시 비교한다.
- case 2-2) 는 X의 마지막 원소와 Z의 마지막 원소와 같은 경우이다. 이 경우, Y의 마지막 원소를 없애고 다시 비교한다.
아래 그림은 case 2-1)과 case 2-2)의 경우를 나타낸 것이다.

위와 같은 두가지 경우를 recurrence 로 표현하면 아래와 같다. 이 recurrence를 가지고 두가지 풀이방법을 통해 LCS문제를 해결할 수 있다.
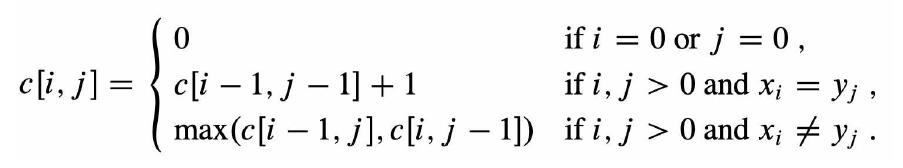
3-1. Recursive한 풀이
LCS recurrence 식을 가지고 재귀적으로 함수를 호출하여 푸는 방식이다. 코드로 나타내면 아래와 같다.
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1)
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n))
Recursive한 풀이방법은 구현이 간단하다는 장점이 있지만, 함수가 recursive하게 호출되므로 성능이 좋지 않다는 단점이 있다.
3-2. Dynamic Programming을 사용한 풀이
DP(Dynamic Programming) 방식은 전체 문제를 여러가지 작은 무제로 쪼개고, 작은 문제들의 답을 저장하여 보다 효율적으로 문제를 해결하는 방식이다.
가장 직관적으로 푸는 방법은 바로 아래 그림처럼 표를 그리는 것이다.
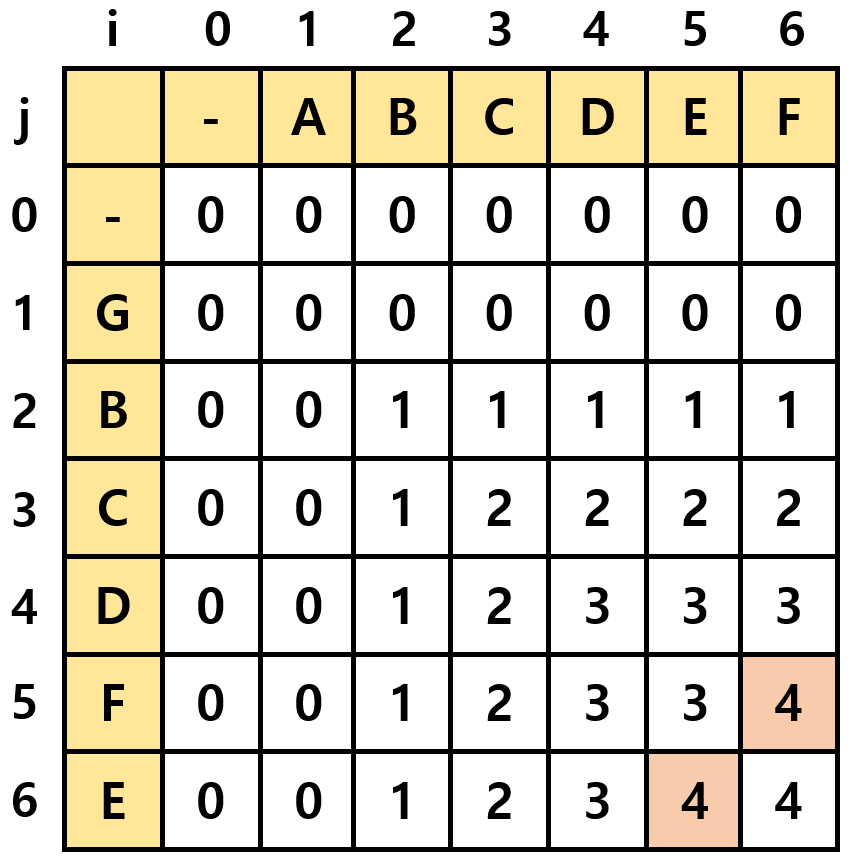
X = "ABCDEF", Y = "GBCDFE" 라고 예시를 들어보자.
우선 가로축과 세로축에 각각 X, Y 배열을 작성한 뒤, 계산을 위해 0행과 0열은 모두 0으로 채워준다.

이제 (1, 1) 부터 하나씩 차근차근 채워나가면 된다. 채우는 방법은 앞서 구한 recurrence 식을 이용하면 된다.
X1인 "A" 와 Y1 인 "G" 는 서로 다르므로, Case 2) 에 해당하며, 이 경우 max(c[i-1, j], c[i, j-1]) 이다.
c[i-1, j]와 c[i, j-1]은 표에서 모두 0이므로 (1,1)도 0이 된다.

다음으로 (2, 2)를 채워보도록 하자.
X2인 "B"와 Y2인 "B"가 서로 같으므로, Case 1) 에 해당하며, 이경우 c[i-1, j-1] + 1 이다.
c[i-1, j-1]은 표에서 (1, 1) 이므로 0 이다. 따라서 0 + 1 = 1 이 된다.

이런 식으로 아래 그림과 같이 표를 모두 채워나갔을 때, 가장 큰 수가 바로 LCS가 된다.
본 예시에서 LCS 값은 4이며, "BCDF"와 "BCDE"이다.
그리고 바로 이 방식이 Dynamic Programming을 이용한 LCS의 풀이법이다.
해당 과정을 코드로 구현해보면 다음과 같다.
def LCS_dp(X, Y, m, n):
table = []
for i in range(0, m+1):
line = []
for j in range(0, n+1):
line.append(0)
table.append(line)
for i in range(0, m):
for j in range(0, n):
if X[i] == Y[j]:
table[i][j] = table[i-1][j-1] + 1
elif table[i-1][j] >= table[i][j-1]:
table[i][j] = table[i-1][j]
else:
table[i][j] = table[i][j-1]
return table
X = ["A", "B", "C", "D", "E", "F"]
Y = ["G", "B", "C", "D", "F", "E"]
result = LCS_dp(X, Y, len(X), len(Y))
print(result)
3. 시간 복잡도
앞서 우리는 Recursive 한 방식과 Dynamic Programming을 이용한 LCS의 풀이를 살펴보았다.
Recursive 한 방식의 시간복잡도 : O(mn)
Dynamic Programming 방식의 시간복잡도 : O(m + n)
따라서 DP를 이용한 풀이가 성능이 훨씬 좋은 것을 확인할 수 있다.
위 내용은 공부하며 작성한 것으로, 오류가 있을 수 있습니다.
'프로그래밍, 알고리즘' 카테고리의 다른 글
| [알고리즘] Activity Selection (Greedy Algorithm 활용) (0) | 2021.11.24 |
|---|---|
| [알고리즘] Quick Sort 의 개념 (0) | 2021.10.26 |
| [알고리즘] Maximum-subarray 구하기 (Divide-and-conquer 활용) (0) | 2021.10.23 |
| [알고리즘] Merge sort (Divide-and-conquer 활용) (0) | 2021.10.03 |
| [알고리즘] Insertion sort 란? (0) | 2021.09.24 |




