shine's dev log
[알고리즘] Merge sort (Divide-and-conquer 활용) 본문
1. Merge sort 코드
def mergesort(l):
if len(l) < 2:
return l
mid = len(l) // 2
left = mergesort(l[:mid])
right = mergesort(l[mid:])
if left and right:
return merge(left, right)
def merge(left, right):
left.append(99999) # Suppose 99999 is infinite.
right.append(99999) # Suppose 99999 is infinite.
index1 = 0
index2 = 0
temp = []
while left[index1] != 99999 or right[index2] != 99999:
if left[index1] >= right[index2]:
temp.append(right[index2])
index2 += 1
else:
temp.append(left[index1])
index1 += 1
return temp
l = [38, 27, 43, 3, 9, 82, 10]
result = mergesort(l)
print(result)
위의 코드는 Merge sort의 python 코드다.
2. 기본 알고리즘
Merge sort는 기본적으로 Divide-and-Conquer 알고리즘을 이용한다.
Divide-and-Conquer 알고리즘은 이름에서 알 수 있듯이 전체의 문제를 여러 새끼문제들로 나누고, 그 새끼문제들을 하나씩 해결해나가면서 전체의 문제를 해결해나가는 알고리즘이다.
Merge sort에서는 아래와 같이 적용된다.
1) 전체의 sequence를 절반으로 쪼갠다.
2) 각 sub-sequence의 크기가 1이 될 때까지 반복한다.
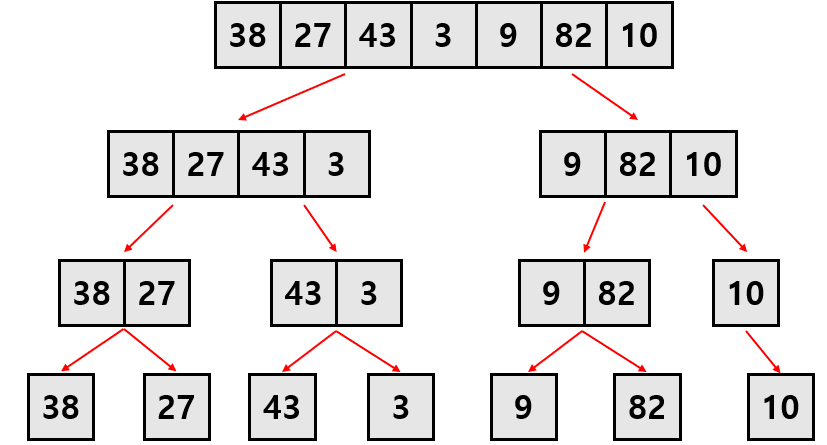
사실 전체 sequence를 크기가 1이 될 때까지 쪼개는 과정은 간단하다. 핵심적인 부분은 쪼개진 녀석들을 merge 하면서 정렬하는 단계인데, 다음과 같은 방법을 사용한다.
3) merge 하려는 두 sub-sequence의 가장 왼쪽에 있는 원소 중 더 작은 원소를 선택하여 정렬한다.
4) merge 하려는 두 sub-sequence가 모두 merge 될 때까지 반복한다.
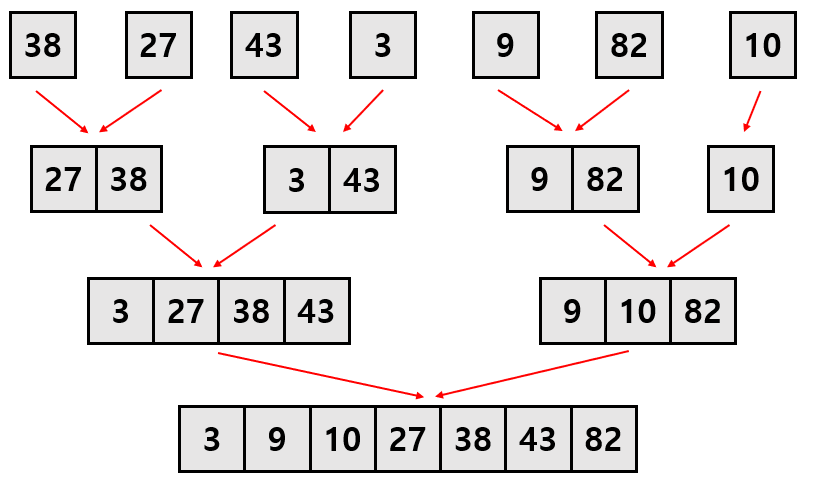
다시 코드를 살펴보자.
def mergesort(l):
if len(l) < 2:
return l
mid = len(l) // 2
left = mergesort(l[:mid])
right = mergesort(l[mid:])
if left and right:
return merge(left, right)
위의 예시에서 전체 sequence를 크기가 1이 될 때까지 쪼개는 과정을 mergesort( ) 라는 함수를 통해 구현하였으며, 보다 효율적이고 정확한 처리를 위해 recursive하게 mergesort( ) 함수를 사용하였다.
만약 크기가 1이 된다면, 2 ~ 3 번째 줄에 의해 리턴하게 되고, 10번째 줄의 merge( ) 함수를 호출한다.
merge( ) 함수는 위의 예시에서 3) 4) 단계를 담당한다. 즉, 쪼개진 두 sub-sequence를 순서대로 정렬하는 과정이다.
코드는 아래와 같다.
def merge(left, right):
left.append(99999) # Suppose 99999 is infinite.
right.append(99999) # Suppose 99999 is infinite.
index1 = 0
index2 = 0
temp = []
while left[index1] != 99999 or right[index2] != 99999:
if left[index1] >= right[index2]:
temp.append(right[index2])
index2 += 1
else:
temp.append(left[index1])
index1 += 1
return temp
해당 코드는 merge 함수에 들어온 두개의 sub-sequence의 끝에 무한대(여기서는 99999)를 추가하고, 각 sub-sequence의 첫번째 원소부터 비교하여 정렬을 수행하는 과정을 담고 있다.
3. 시간복잡도
Merge sort의 시간 복잡도의 경우, n log n 이다.
merge sort의 경우, 전체 sequence가 어떤 식으로 배열 되어있던간에, 정렬하는데 걸리는 전체 비교 횟수는 동일하므로 best case, worst case 모두 n log n의 시간복잡도를 가진다.
'프로그래밍, 알고리즘' 카테고리의 다른 글
| [알고리즘] Quick Sort 의 개념 (0) | 2021.10.26 |
|---|---|
| [알고리즘] Maximum-subarray 구하기 (Divide-and-conquer 활용) (0) | 2021.10.23 |
| [알고리즘] Insertion sort 란? (0) | 2021.09.24 |
| [python] face_recognition 라이브러리 pyinstaller 사용시 RuntimeError 오류 해결 (0) | 2021.05.20 |
| [C] 깊은복사와 얕은복사 (deep copy, shallow copy) (0) | 2020.07.16 |




