Shine's dev log
PCA (Principal Component Analysis) : 주성분 분석 이란? 본문
1. PCA (주성분 분석)
PCA는 대표적인 dimensionality reduction (차원 축소)에 쓰이는 기법으로, 머신러닝, 데이터마이닝, 통계 분석, 노이즈 제거 등 다양한 분야에서 널리 쓰이는 녀석이다.
쉽게 말해 PCA를 이용하면 고차원의 데이터를 낮은 차원의 데이터로 바꿔줄 수 있다는 것인데, 중요한 것은 "어떻게 차원을 잘 낮추느냐" 이다.
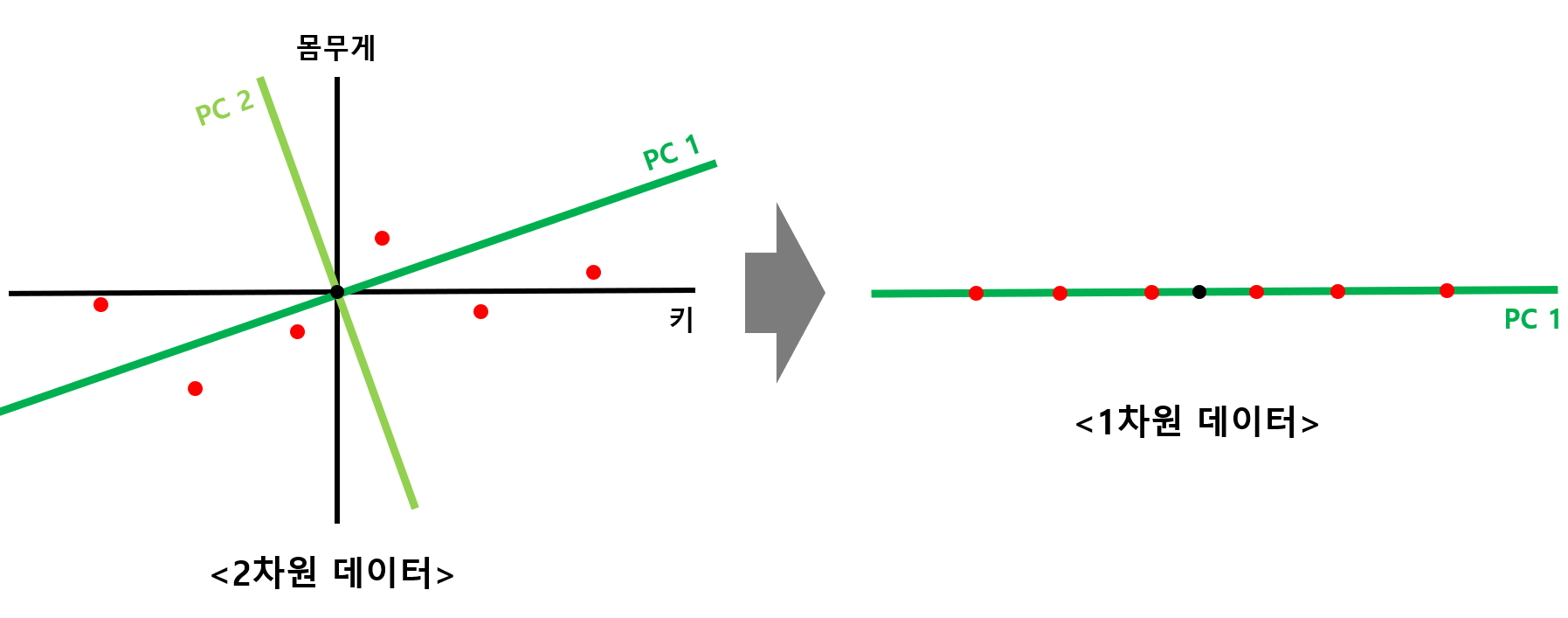
예를 들어 아래 [그림 1] 에서 왼쪽에 있는 2차원 데이터를 오른쪽에 있는 1차원 데이터로 바꾼다고 생각해보자.

아무리 잘 바꾼다고 하더라도, 2차원의 데이터의 특징을 모두 살리면서 1차원의 데이터로 바꿔줄수는 없을 것이다.
그렇다면 차선책으로, 모든 특징을 살릴 수는 없을지라도 최대한 특징을 살리며 차원을 낮춰주는 방법을 고안하기 시작했고, 그 중 하나가 바로 PCA 이다.
지금부터 PCA 알고리즘에 대한 직관적인 해석과 수학적인 해석을 알아보도록 하자.
2. PCA 알고리즘의 직관적인 해석
이번 장에서는 PCA 알고리즘이 어떻게 차원을 "잘" 낮춰주는지 직관적인 해석을 통해 알아볼 것이다.
설명에 사용되는 예시는 2차원 데이터를 1차원으로 낮춰주는 상황으로 가정한다.
아래 [그림 2]의 표와 같은 데이터가 있다고 생각해보자. 각 cloumn 은 사람들의 키와 몸무게에 대한 정보를 의미하며, 각 row는 여러 사람들의 샘플을 의미한다.
해당 표의 데이터를 2차원 평면상에 나타내보면 오른쪽 그래프와 같이 될 것이다.

이제 PCA 알고리즘을 통해 2차원 데이터를 1차원으로 낮춰보자.
STEP 1) 각 축에 대한 평균값을 구한 뒤, 해당 점이 원점이 되도록 shift 해준다.

[그림 3] 에서 볼 수 있듯이 데이터의 x축, y축에 대한 평균값을 구해준 뒤, 각 평균값에 해당하는 점들의 교차점이 원점이 되도록 전체 데이터를 shift 해준다.
STEP 2) 데이터에서 원점을 지나는 직선에 수선의 발을 내려, 해당 길이가 최대가 되는 직선을 찾는다.
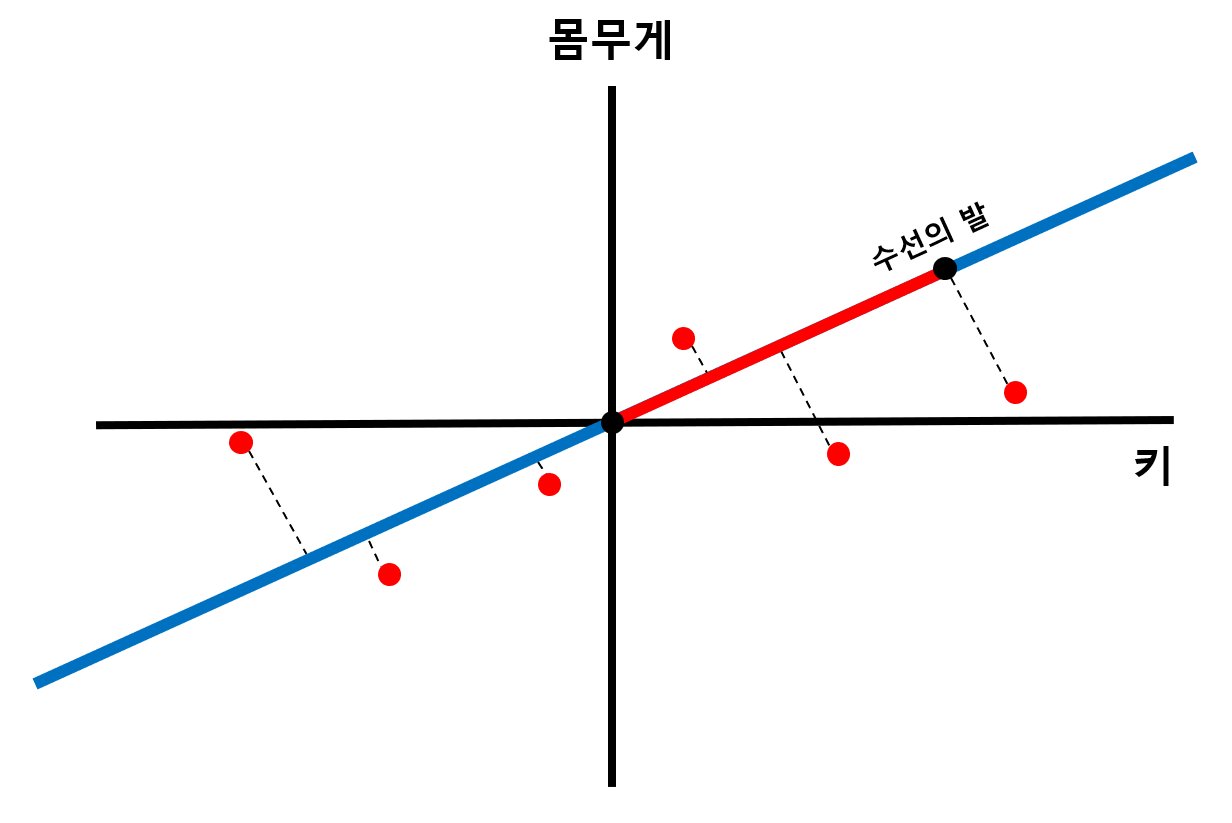
위 그림처럼 모든 데이터에서 원점을 지나는 직선에 수선을 발을 내리면, 원점으로부터 수선의 발까지의 길이를 구할 수 있게 된다. (빨간 직선. [그림 4]에서는 한 점에대한 길이만 구했지만, 실제로는 모든 점에 대한 길이를 구해야 한다.)
원점을 지나는 직선의 기울기가 변함에 따라, 이 빨간선들의 길이 또한 변하게 된다. PCA 에서는 이 빨간선들의 길이 제곱들의 합이 최대가 되는 직선을 찾는다. (앞으로 빨간선들의 길이합을 SS(Sum of Squares) 라고 부를 것이다.)
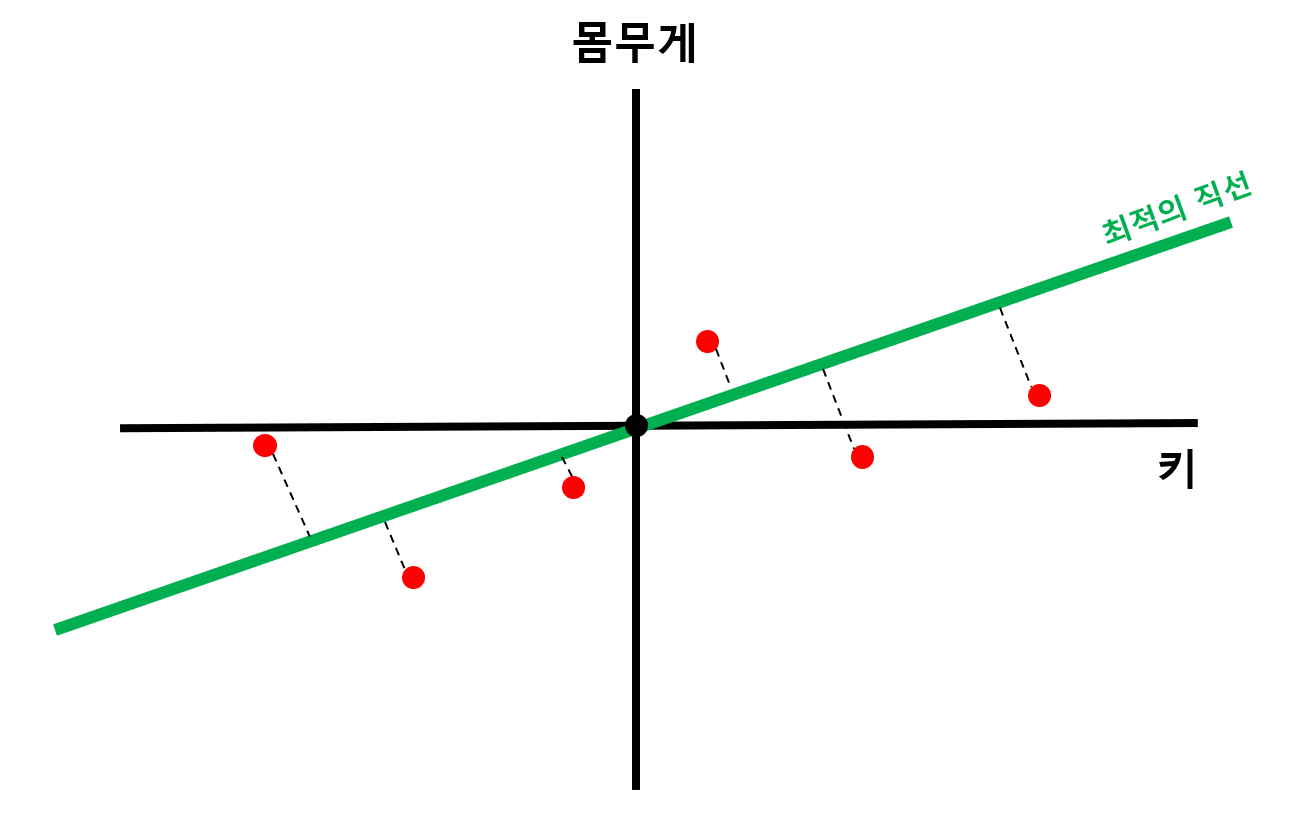
길이 합이 최대가 되는 최적의 직선을 찾다보면, 얼추 [그림 5] 처럼 초록색 직선이 선택될 것이다.
STEP 3) 찾은 직선을 PC1으로 설정하고, loading score 구한다.
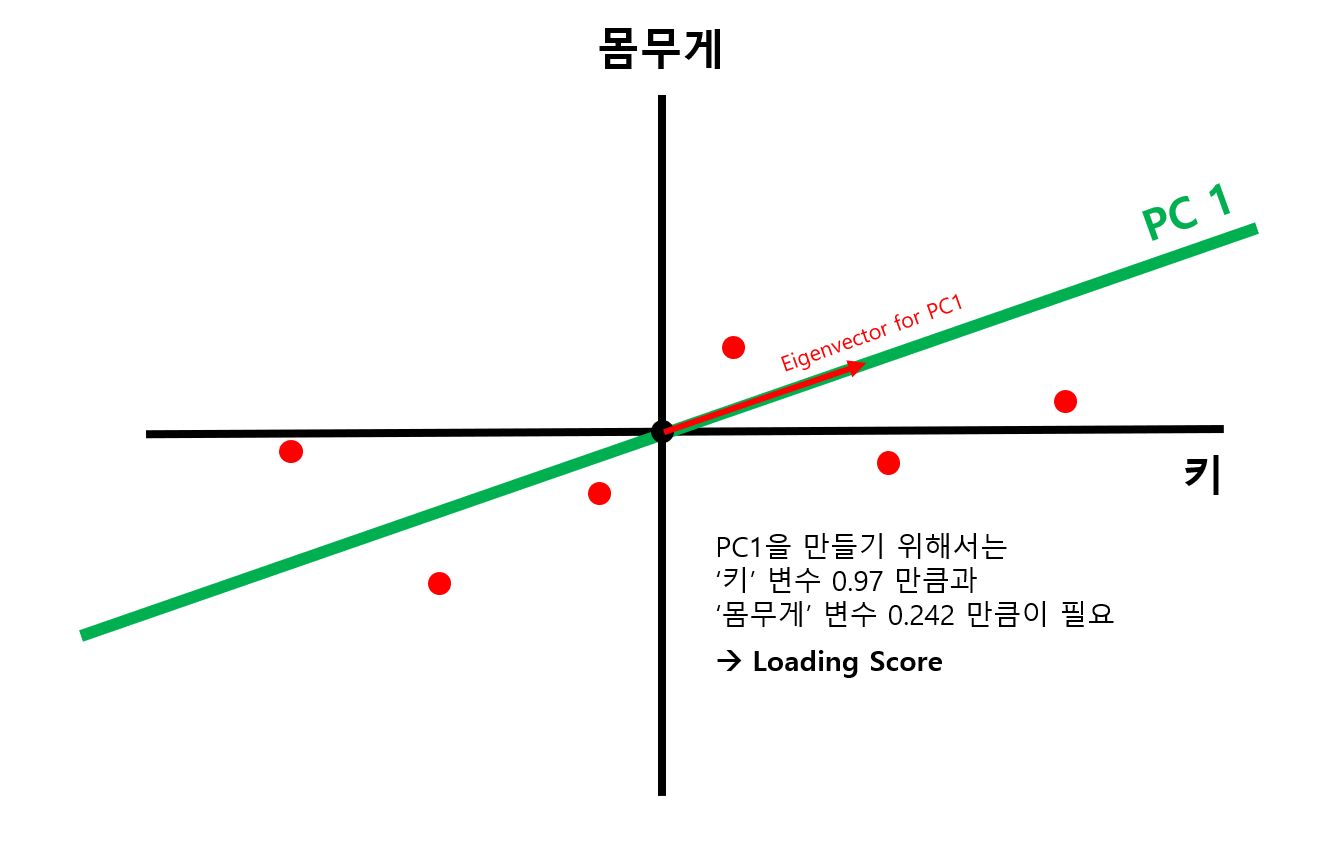
아까 그림에서의 초록색 직선을 PC1으로 잡는다.
이때 PC1과 방향이 같은 벡터를 "PC1의 Singular vector" 혹은 "PC1의 Eigenvector" 라고 한다.
또한, PC1의 Singular vector의 x 축 길이와 y 축 길이의 비율을 Loading score 라고 한다. [그림 6]에서는 0.97, 0.242 만큼의 비율이 바로 Loading score 이다.
STEP 4) PC1에 직교하는 직선을 PC2로 잡는다.
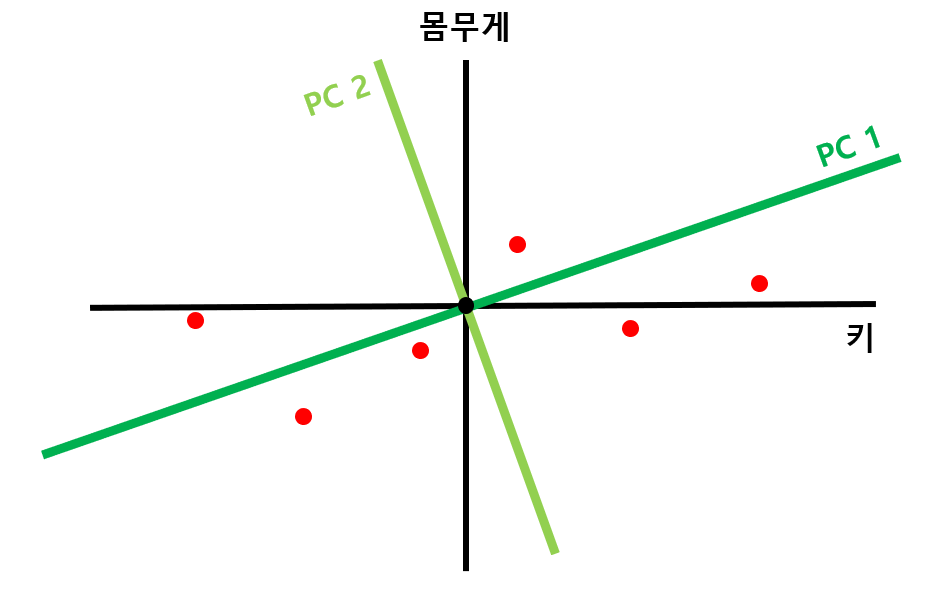
[그림 7] 과 같이 PC1에 직교하는 직선을 PC2로 잡는다.
위의 예시의 경우 2차원이므로 PC1에 직교하는 직선이 유일하지만, 만약 3차원의 경우라면, PC1에 직교하는 직선이 평면으로 나올 것이다. 이 경우에는, PC1에 직교하는 평면 중에서, STEP 2) 의 과정을 다시 거쳐 수선의 발까지의 거리합이 최대가 되는 직선을 선택해주면 된다.
참고로 N 차원 데이터에는 N 개의 PC 직선이 나오게 된다.
STEP 5) PC1과 PC2를 축으로 하여 회전시킨 뒤, scree plot 생성한다.
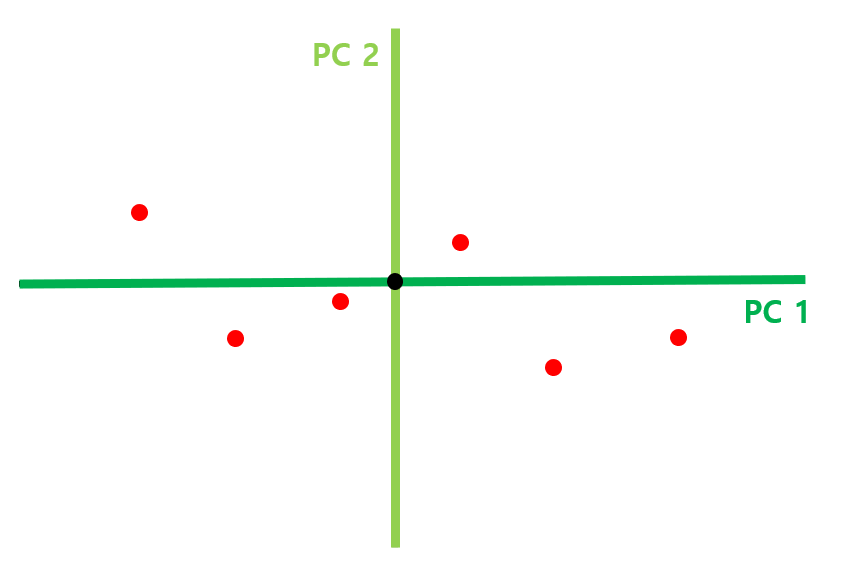
앞서 구한 PC1과 PC2 직선을 각각 x축, y축이 되도록 데이터를 회전시키면 위의 그림과 같이 된다.
이제 각 PC 축이 전체 데이터를 얼마나 잘 표현하고 있는지를 나타내주는 scree plot을 그려보자.
scree plot 을 생성하기 위해, PC1과 PC2의 SS 비율을 구해야 한다. SS 값은 앞서 STEP 2에서 구했었다.
만약 PC1과 PC2의 SS 비율이 8.9 : 1.1 이라고 하면, [그림 9]와 같이 scree plot을 그려줄 수 있다.
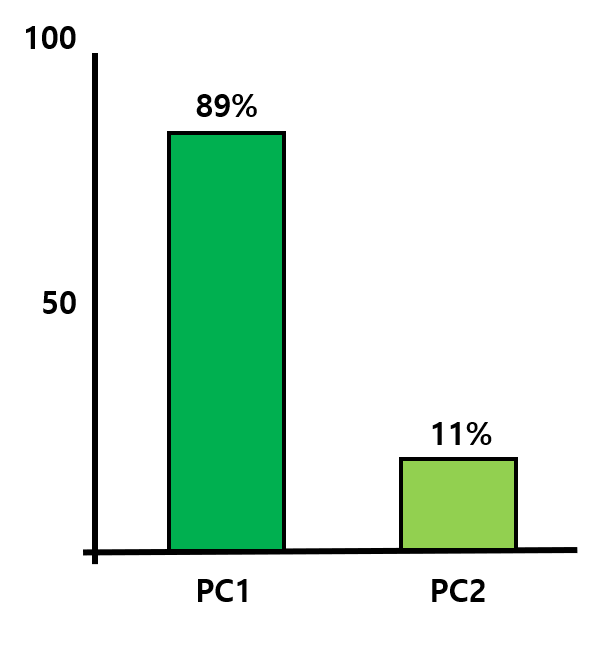
해당 그래프의 의미는 PC1 축이 전체 데이터 특징의 89% 정도를 나타내고 있으며, PC2 축이 전체 데이터 특징의 11% 정도를 나타내고 있다는 뜻이다.
여기서 PCA의 목표를 이룰 수 있게 된다. PCA는 "어떻게 차원을 잘 낮추느냐" 라는 물음에서부터 시작되었다.
만약 89% 정도의 특징만으로도 해당 데이터를 잘 나타낼 수 있을 것이라고 판단되면, PC2 축을 제거하고, PC1 축만을 가지고 1차원으로 나타낼 수 있다.
이렇게 함으로써 2차원의 데이터를 1차원으로 바꿀 수 있는 것이다.
다른 예를 들어, 3차원 데이터가 있는데, PCA를 통해 PC1 PC2 PC3 3개의 축을 잡았고, scree plot 을 그려본 결과 PC1이 73%, PC2가 17%, PC3가 10% 를 차지한다고 해보자. 이러면 개발자에게는 차원을 줄이는 두가지 선택권이 있는 것이다.
1) 데이터 특징의 90% 를 살리며 3차원에서 2차원으로 차원을 축소하는 선택권 (PC1, PC2 선택)
2) 데이터 특징의 73% 를 살리며 3차원에서 1차원으로 차원을 축소하는 선택권 (PC1만 선택)
무엇을 선택할지는 현재 시스템의 리소스 상황을 고려하며 선택하면 된다.
3. PCA 알고리즘의 수학적인 해석
PCA 알고리즘의 수학적인 해석에 들어가기에 앞서, 배경지식으로 covariance matrix, Eigenvector 등에 대하여 살짝 살펴보자.
Background1) Variance
variance, 즉 분산은 쉽게 말해 '데이터가 얼마나 넓게 퍼져있는가' 이다. variance는 편차의 제곱합의 평균으로 구할 수 있다.
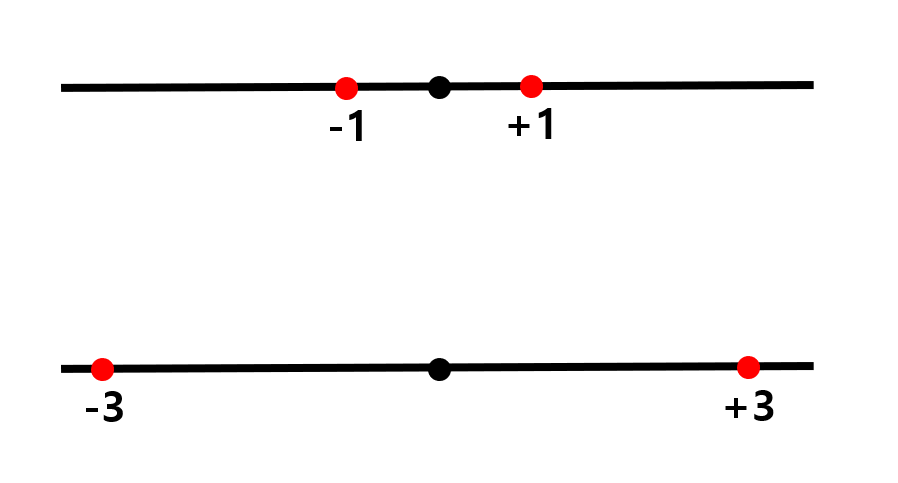
위의 평균이 모두 0인 1차원 데이터를 나타낸 [그림 11] 에서, 위의 데이터의 variance는 (1+0+1)/3 = 2/3이고, 아래 데이터의 variance는 (9+0+9)/3 = 6 이다.
Background2) covariance
covariance는 고차원에서의 데이터들 간의 variance를 나타내는 값이다.
앞서 1차원 데이터에서의 분산을 구해봤다. 그렇다면, 2차원 데이터에서의 분산은 어떻게 구할까?
답은 "x축에서의 variance와 y축에서의 variance를 융합하면 된다" 이다.
그럼 어떻게 두 variance를 융합해야 할지가 고민이다. 그냥 x축에서의 variance와 y축에서의 variance를 더하면 될까?
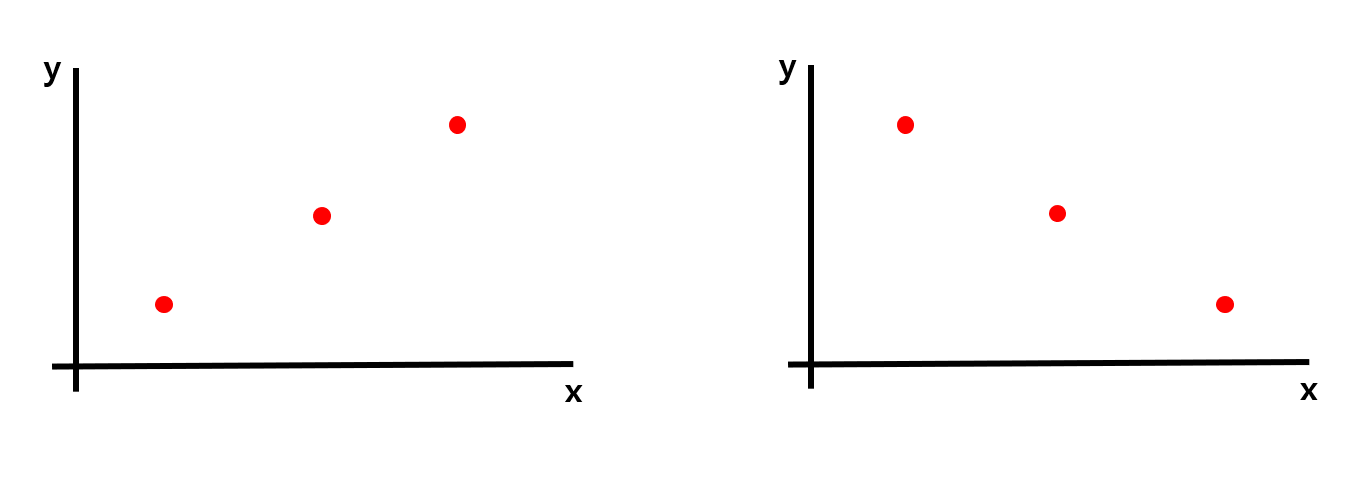
[그림 12] 와 같은 데이터가 있다고 가정해보자. 오른쪽과 왼쪽의 데이터의 x축에서의 variance와 y축에서의 variance는 모두 같을 것이므로 단순히 두 variance를 더한 값도 같을 것이다.
하지만 위의 두 데이터는 완전히 다른 분포를 나타내는 데이터이지만, covariance가 같아지므로, 단순히 더하는 방법은 옳지 않은 방법이다.
이런 문제를 해결하기 위해 covariance를 구하는 방식은 x값과 y값을 각각 x, y값의 평균의 차 곱하여 더하고(= 내적) n으로 나눠줌으로써 구할 수 있다.
(나중에 말하겠지만, 이 방식은 평균이 0일때만 유효하다. 일반적인 경우는 [수식 1]을 따른다.)
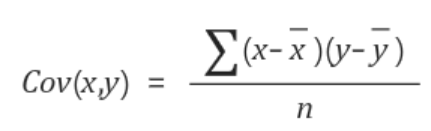
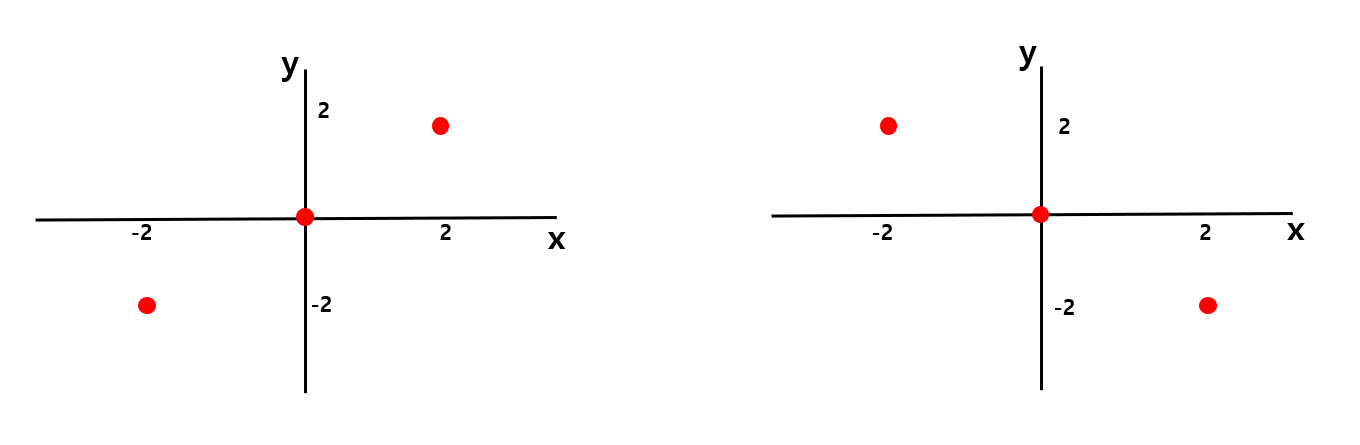
[그림 13]과 같은 데이터가 있다고 해보자. 왼쪽 데이터의 x값과 y값을 곱하면 각각 +4, 0, +4가 된다. 그리고 이 값들을 모두 더해 데이터개수로 나눠주면 covariance가 된다.
즉, 왼쪽 데이터의 covariance는 (+4+0+4)/3 = +8/3 이고, 오른쪽 데이터의 covariance는 (-4+0-4)/3 = -8/3 이 된다.
※ 참고 ※
covariance를 구하기 위해 내적하는 과정은 데이터의 평균값이 0 일때만 유효하다. 2차원 데이터일 경우, 데이터의 x축 평균과 y축 평균이 모두 0이어야 하며, 0이 아닐 경우 각각 평균값을 빼주면 된다. (앞서 직관적인 해석에서 본 STEP 1) 과정과 일치)
Background3) covariance matrix
covariacne 값을 통해 covariance matrix 라는 행렬을 만들어 낼 수 있다. 시그마 기호로 표현하는 2차원 데이터에서의 covariance matrix의 정의는 다음과 같다.
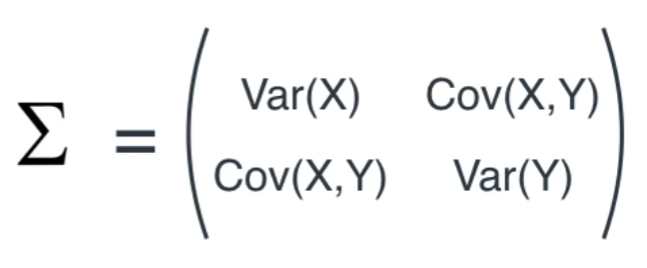
행렬의 주대각선은 각 변수의 variance를 나타내며, i행 j열 데이터는 i와 j 변수의 covariance를 나타낸다.
물론 i와 j 변수의 covariance와, j와 i 변수의 covariance 는 같으므로 covariance matrix는 주대각선을 축으로 대칭인 symmetric 한 형태가 될 것이다.
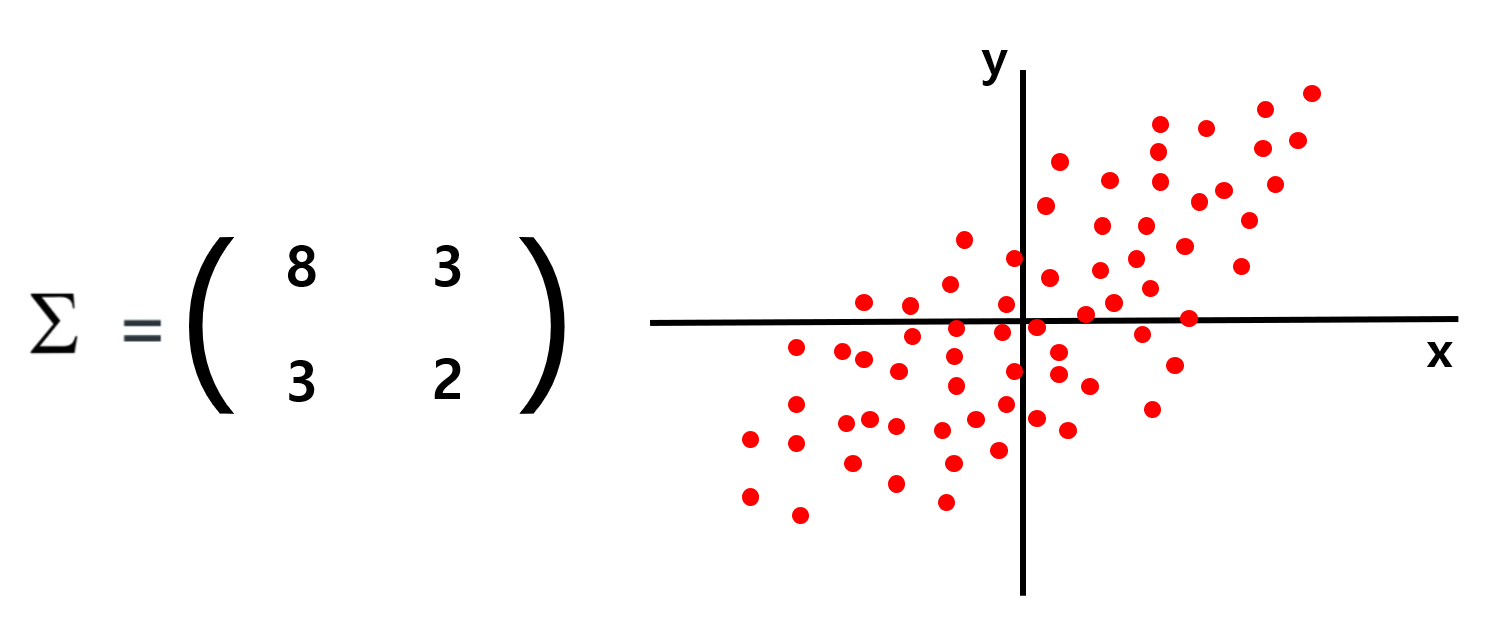
예를들어 [그림 15] 와 같은 covariance matrix가 있다고 해보자. x의 variance는 y의 variance보다 크므로 데이터는 가로로 길쭉한 형태가 될 것이며, x와 y의 covariance가 양수이므로 1, 3 사분면을 지나는 오른쪽 그림과 같은 형태가 될 것이다.
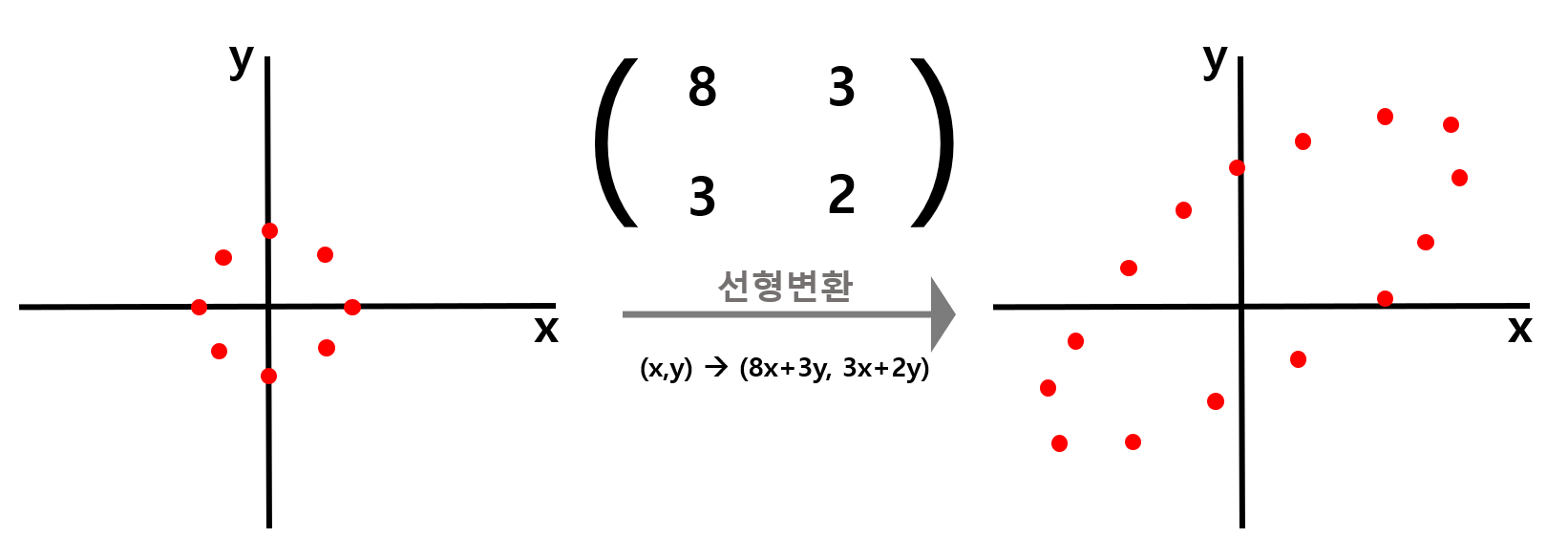
다른 관점에서 바라보면, covariance matrix는 선형변환 관점에서 바라보기도 한다.
[그림 16] 과 같이 원점을 기준으로 골고루 퍼져있는 normal distributied 데이터에 covariance matrix를 곱해서 선형변환을 수행해주면, 아까 봤던 것처럼 covariance matrix의 특성에 맞게 데이터가 쭉 늘어나는 형태로 변하는데, 이렇게 늘어나는 것을 shearing 이라고 한다.
Background4) Eigenvector, Eigenvalue
eigenvector(고유벡터) 라는 놈은 행렬 A 에 의해 Linear Transformation(선형변환) 되는 수많은 벡터들 중에, 변환되기 전과 변환된 후의 벡터 방향이 똑같은 벡터이다.
예를 들어 아까 살펴본 covariance matrix를 행렬 A라 하고 선형변환을 시켜보겠다.
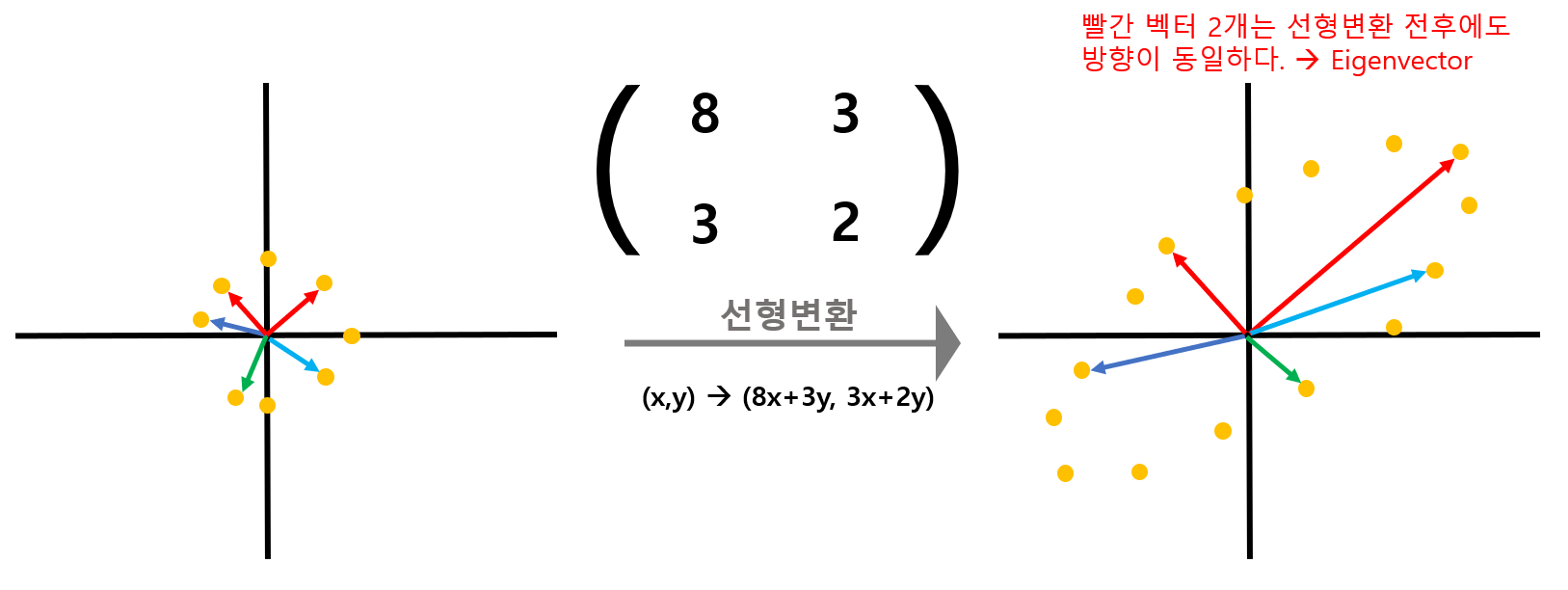
[그림 17] 과 같이 단위원을 이루던 벡터는 오른쪽과 같이 1,3사분면에 걸쳐있는 넙적한 찌그러진 원이 될 것이다.
변환된 수많은 벡터들 중, 빨간색으로 표시된 벡터 2개만은 변환 전과 후의 방향이 동일하다.
저 빨간 두개의 벡터가 해당 선형 시스템 방정식에 대응하는 Eigenvector이며, 이때 Eigenvecotr의 변환 전과 후의 길이 변화 비율을 Eigenvalue라고 한다.
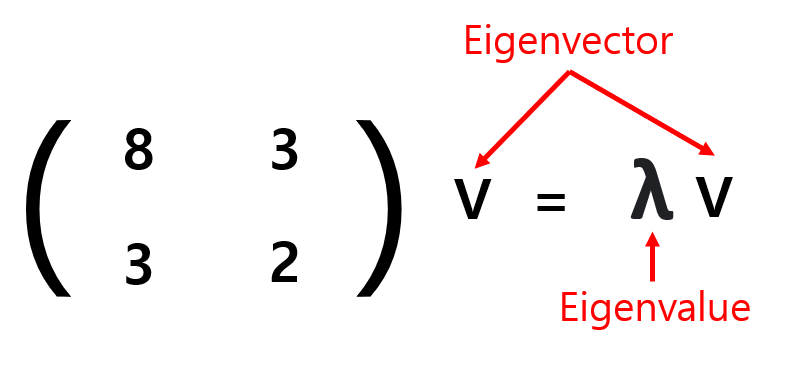
이를 수식으로 나타내보면 [그림 18] 과 같다. 선형 변환이 되기 전과 후의 방향이 같은 벡터 v가 Eigenvector이며, 변화되는 길이의 비율 λ값이 Eigenvalue이다.
참고로 N 차원 데이터에서는 N개의 Eigenvector/Eigenvalue가 나온다. 위의 예시에서는 2차원 데이터였으므로 2개의 Eigenvector/Eigenvalue가 나온 것이다.
이제 PCA 알고리즘의 수학적인 해석에 필요한 기본 지식은 끝났다. 이 배경지식만 있으면 정말 손쉽게 PCA를 수학적으로 이해할 수 있다.
STEP 1) 고차원의 데이터의 covariance matrix를 구한다.
앞서 covariance matrix를 어떻게 구하는지는 이미 알아보았으므로 쉽게 할 수 있을 것이다.
STEP 2) 구한 covariance matrix에서 Eigenstuff(Eigenvector, Eignevalue)를 구한다.
covariance matrix를 가지고 선형변환을 한 이전과 이후의 방향이 같은 벡터가 Eigenvector, 그 길이 변화 비율을 Eigenvalue라고 한다고 앞서 알아보았다.
STEP 3) 구한 Eigenstuff를 Eigenvalue가 큰것부터 작은 순서대로 정렬한다.
이쯤되면 눈치를 챘을 것이다. 앞서 직관적인 해석에서 알아보았던 PC1, PC2, ... 축 들이 바로 여기서 구한 Eigenvector들이다.
또한, 앞서 직관적인 해석에서 알아보았던 scree plot에서 각 PC들이 가졌던 비율들이, 바로 여기서 구한 Eigenvalue 값들의 비율이다.
즉, Eigenvalue가 큰 것부터 작은 순서대로 정렬한 것이 일종의 scree plot을 그린 것이라고 보면 된다.
STEP 4) 원하는 만큼 Eigenvector를 쳐냄으로써 차원 축소를 해준다.
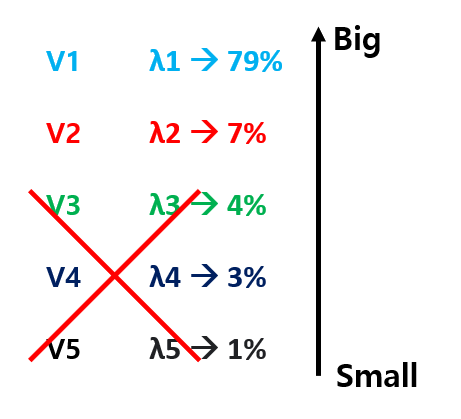
만약 5차원 데이터에서 Eigenstuff를 구한 뒤, Eigenvalue를 기준으로 정렬했다고 해보자. 그럼 [그림 19] 와 같이 5개의 Eigenstuff가 보일 것이다.
여기서 만약 내가 5차원 데이터를 2차원으로 줄이겠다! 라고 한다면, Eigenvalue가 큰 두개를 빼고 나머지 3개를 쳐내면 된다.
그러면 두개의 Eigenvector를 축으로 하는 2차원 데이터로 차원을 줄일 수 있으며, 해당 2차원 데이터가 나타내는 데이터의 특징은, 두 Eigenvector v1, v2 의 Eigenvalue가 가지는 비율인 86%가 된다.
앞서 알아보았던 PCA의 직관적인 해석과 수학적인 해석은 결국 같은 의미를 가지는 것이었다. 이 전체적인 과정을 단계적으로 나타내보면 다음과 같다.
1) N차원의 데이터로부터 Covariance matrix를 생성한다.
2) 생성된 covariance matrix에서 N개의 Eigenvector, Eigenvalue를 찾는다.
3) 찾은 Eigenvector를 Eigenvalue가 큰 순서대로 정렬한다.
4) 줄이기 원하는 차원 개수만큼의 Eigenvector만 남기고 나머지는 쳐낸다.
5) 남은 Eigenvector를 축으로 하여, 데이터의 차원을 줄인다.
이 과정을 PCA 라고 한다.
'머신러닝' 카테고리의 다른 글
| [Pytorch] GAN 구현 및 학습 (2) | 2022.03.12 |
|---|---|
| [ML] Deepfake Detection 성능 분석 (8) | 2022.02.26 |
| KL divergence와 JSD의 개념 (feat. cross entropy) (1) | 2022.02.19 |
| [Recommender system] 영화 추천 시스템 (0) | 2022.01.23 |
| Association Rules(Support, Confidence, Lift, A-priori 알고리즘) (1) | 2021.12.01 |




