라우팅 알고리즘 (Dijkstra's 알고리즘, Bellman-Ford 알고리즘)
1. 라우팅 알고리즘
라우팅 알고리즘에는 크게 두가지 종류가 있다.
전체적인 네트워크 상황을 알고, 이를 토대로 라우팅 경로를 판단하는 Link State 알고리즘,
특정 라우터와 연결된 이웃 라우터의 정보만을 가지고 판단하는 Distance Vector 알고리즘이다.
이번에는 Link State 알고리즘의 대표적인 예시인 Dijkstra's 알고리즘과, Distance Vector 알고리즘의 대표적인 예시인 Bellman-Ford 알고리즘을 살짝 살펴보자.
2. Dijkstra's 알고리즘
전체 네트워크 환경의 정보를 안다는 가정 하에서 사용할 수 있는 알고리즘이다.
바로 예시를 통해 알아보자.
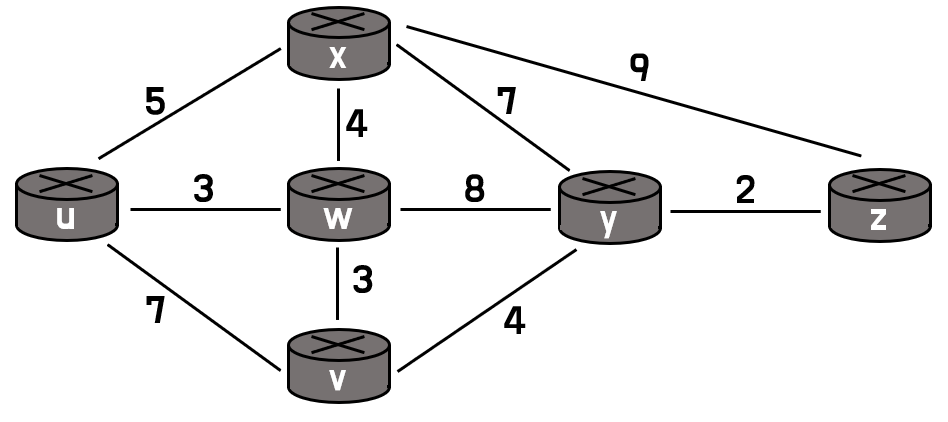
[그림 1] 같은 네트워크 상황이 있다고 가정하자.
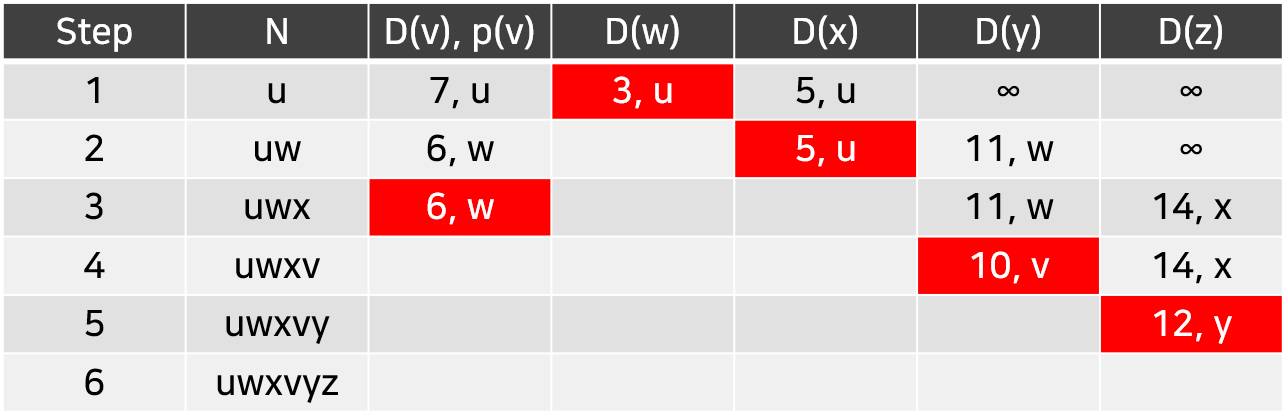
처음에 u 노드에서 시작한다고 하면, u 노드에서 갈 수 있는 노드들의 값들을 계산해보면, [표 1]의 step1 행의 값들과 같다. 이 중에서 가장 cost가 적은, w 노드로 가는 길이 처음으로 선택될 것이다.
다음으로, w 노드로 가는 길이 선택됨과 동시에, 다시 u 노드에서 갈 수 있는 노드들의 값들을 계산해보면, [표 1]의 step2 행의 값들과 같다.
이때, u에서 v로 가는 경로의 cost의 경우, 직접 가는 길과 이미 알려진 w를 거쳐 가는 길 중 cost가 적은 값을 기준으로 다시 업데이트 된 것을 확인할 수 있다. (cost 7 -> cost 6)
결국 step2 에서는 가장 cost가 적은 x 노드로 가는 길이 선택될 것이다.
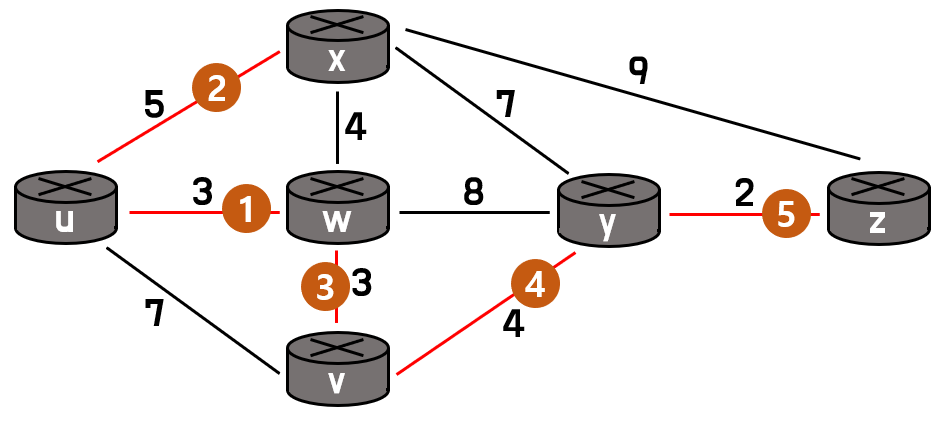
이런 과정으로 계속해서 진행하면 [표 1]과 같은 값들이 나올 것이고, 이를 통해 만들어진 그래프는 아래 [그림 2]와 같다.
3. Bellman-Ford 알고리즘
다음으로, Distance Vector 알고리즘의 대표적인 알고리즘인 Bellman-Ford 알고리즘을 알아보자.
해당 알고리즘은 전체 네트워크 상황이 아닌, 자신과 인접한 라우터의 상황만 알 때 사용 가능하다.
역시 바로 예시를 통해 알아보자
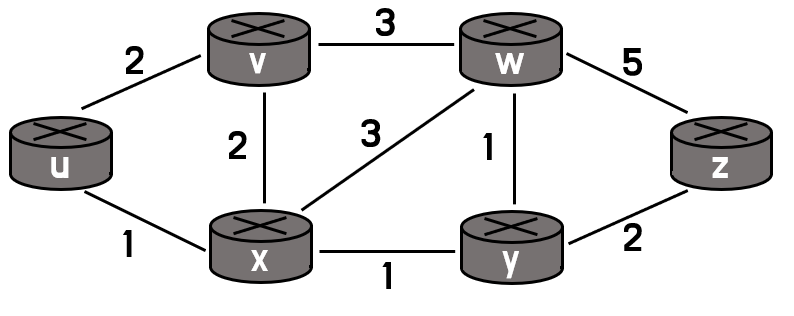
[그림 3]과 같은 네트워크 상황이 있다고 가정하자.
u노드에서 z노드로 가는 최단 경로를 찾고싶다고 할 때,
step 1. 우선, Dv(z) = 5, Dx(z) = 3, Dw(z) = 3 임을 계산한다.
(Dx(y) 는 x에서 y까지 가는 최단경로)
step 2. Du(z)를 아래 식을 이용해 계산한다.
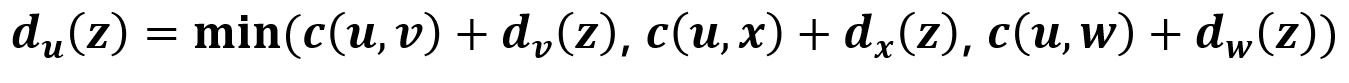
위의 식을 통해 u 노드에서 z 노드로 가는 최단 경로를 찾을 수 있다.
하지만, 여기서 의문인 점이 있는데, step 1 의 Dv(z), Dx(z), Dw(z)의 값들은 어떻게 구하냐는 것이다.
Bellman-Ford 알고리즘은 기본적으로 Distance Vector 알고리즘이므로, 해당 값들은 그냥 이미 알고 있는다고 가정하고 진행하기 때문에 u 노드 입장에서는 이를 전혀 신경쓰지 않는다.
Dv(z)의 경우, v 노드에서 위의 step1, 2 과정을 거쳐 나온 결과가 5인 것이며, u 노드는 이 정보를 이용할 뿐, 구체적으로 어떤 과정을 통해 해당 값이 나왔는지는 고려하지 않는다.
오늘 배운 내용을 정리해보면,
1. Link State 라우팅 알고리즘에는 Dijkstra's 알고리즘이 있다.
2. Distance Vector 라우팅 알고리즘에는 Bellman-Ford 알고리즘이 있다.
위 내용은 공부하며 작성한 것으로, 오류가 있을 수 있습니다.