KL divergence와 JSD의 개념 (feat. cross entropy)
1. KLD / JSD
얼마전 GAN 논문을 읽는데 KLD, JSD에 관한 내용이 나왔다.
그냥 단순히 두 확률분포 간의 distance를 나타내는 divergence라고 생각했는데, 사실은 이게 아니라 더 심오한 내용이 있어서 정리해보겠다.
2. KL divergence (Kullback-Leibler divergence)
2.1. KL divergence의 의미
위키백과에서는 KL divergence를 다음과 같이 정의하고 있다.
쿨백-라이블러 발산(KLD)은 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다.
쿨백-라이블러 발산은 어떠한 확률분포 P가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q를 P 대신 사용할 경우 엔트로피 변화를 의미한다.
말이 어렵긴 하지만, 간단하게 말해서 두 확률분포의 차이를 계산하는데 사용하는 함수이다.
이산 확률변수와, 연속 확률변수에서 KL divergence를 구하는 수식은 [그림 1]과 같다.

[그림 1]과 같은 수식이 어떻게 나왔는지 살펴보기 위해서 잠시 entropy와 cross entropy 의 의미를 살펴보자.
2.2. Entropy
entropy는 정보량이 생산되는 과정에서, 이를 표현하는데 필요한 최소 자원량의 기댓값이다.
예를 들어 어떤 사람1 이 "aaaaaaaabc" 라는 문자를 보냈다.
사람2 는 "abcdefghij" 라는 문자를 보냈다.
이 두 문자를 비트(0 or 1)로 바꿔야한다고 가정해보자.
사람1의 문자는 a를 '0'으로, b를 '1'로 c를 '01'로 바꿔서 보내면, '00000000101' 로 나타낼 수 있다.
하지만, 사람2의 문자를 위 방법으로 바꿔서 보내면, '01011011001010100110011' 로 나타내야만 한다.
즉, 같은 길이의 문자(정보량)이라고 하더라도, 그 문자 내용이 어떻느냐에 따라서 이를 표현하는데 필요한 최소 자원량(비트수) 은 극명하게 달라질 수 있다.
앞서 entropy란, 특정한 정보량(문자)가 생산될 떄, 이를 표현하는데 필요한 최소 자원량의 기댓값, 즉 평균값 이라고 했었다.
그리고 최소 자원량이라는 목표를 달성하기 위해서는, 자주 나오는 문자 (가령 사람1의 문자에서 문자'a') 를 최대한 짧게 변환해야 한다. 이를 위해 'a'를 0으로 변환했었다.
이렇게 자주 나오는 문자를 최대한 짧게 변환할 때, 유용하게 쓰일 수 있는 함수가 바로 [그림 2]에 보이는 -log x 함수이다.
x축을 확률(1을 넘지 않아야 한다), y축을 비트수 라고 생각해보자.
특정 문자가 나올 확률이 높아질수록(x축에서 1에 가까워 질수록) 비트수는 작아져야 하고, 특정 문자가 나올 확률이 낮아질수록(x축에서 0에 가까워 질수록) 비트수는 커져야 한다.

위 로그함수에 기댓값을 구하기 위해 각 확률변수에서의 확률을 곱해주면 그게 바로 기댓값, 즉 "정보량이 생산되는 과정에서, 이를 표현하는데 필요한 최소 자원량의 기댓값", entropy가 되는 것이다.
따라서 entropy를 나타내는 수식 H는 [그림 3]과 같이 정의된다.
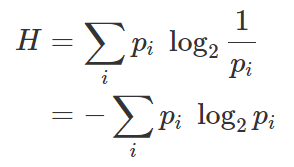
[그림 2]의 수식에서 알 수 있듯이, 특정 정보량을 표현하는데, 특정 확률변수의 확률이 높으면 (p_i가 높으면), 해당 확률변수를 표현할 자원량(log (1/p_i)) 이 줄어들게 된다.
2.2. Cross entropy
Cross entropy는 앞서 살펴본 entropy의 정의에서 살짝만 틀어주면 된다.
앞서 entropy의 수식 [그림 3]에서 p_i 는 특정 확률 변수가 발생할 확률이고, log (1/p_i)는 해당 확률 변수를 표현할 자원량이라 했다.
Cross entropy는 여기서 해당 확률 변수를 표현할 자원량, 즉 log (1/p_i) 값을 P의 확률분포에 따르는 것이 아니라, 임의의 확률분포 Q 에 따르는 것이다.
따라서 Cross entropy의 수식을 나타내보면, [그림 4]와 같다. 바뀐건 log항의 변수가 p에서 q로 바뀐것 뿐이다.
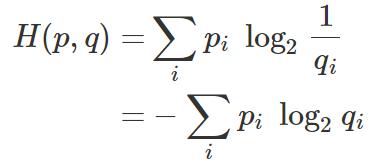
다시 처음의 예시를 적용해 생각해보자.
사람1이 보내려는 "aaaaaaaabc" 라는 문자를 비트로 표현할 때, 자주 나오는 문자를 짧은 비트로 변환하기 위해 log (1/p_i) 를 사용했었는데, 이 값은 확률 p_i 의 크기에 따라 최적화되어 결정되는 값이었다.
하지만, cross entropy 에서는 문자를 변환하기 위한 길이를 사람1이 보낸 문자를 바탕으로 결정하는 것이 아니라, 사람2가 보낸 문자 "abcdefghij"를 바탕으로 결정하는 것이다.
하지만 이렇게 결정할 경우, 자주 쓰이는 문자가 짧은 비트로 변환된다는 보장이 사라지게 되고, 따라서 수식의 결과 값이 증가하게 될 것이다.
즉, 정리해보면,
entropy는 확률분포 P를 따르는 환경에서 정보량이 생산될 때, 이를 표현하는데 필요한 최소 자원량의 기댓값이며,
corss entropy는 확률분포 P를 각각 따르는 환경에서 정보량이 생산될 때, 확률분포 Q를 따르는 환경이라 생각하고 정보량을 표현하는데 필요한 자원량의 기댓값인 것이다.
말로 설명하려니 너무 힘들다
추가적으로, P를 실제 데이터의 확률분포, Q를 내가 만든 머신러닝 모델이 추측한 확률분포라 가정해보자.
P는 [0, 0, 1] 이런식으로 나올 것이고, Q는 [0.1, 0.2, 0.7] 이런식으로 나올 것이다.
이제 P와 Q에 대해 cross entopy를 적용해보면, 왜 사람들이 머신러닝 학습 과정에서 cost function으로 cross entropy를 쓰는지 알 수 있다.
2.4. KL divergence의 진짜 의미
이때까지 살펴본 내용에 의하면, "어떠한 확률분포 P가 있을 때, 샘플링 과정에서 확률분포 P를 사용할 경우의 엔트로피" 는 확률변수 P의 엔트로피, 즉 H(p) 이다.
또한, "어떠한 확률분포 P가 있을 때, 샘플링 과정에서 확률분포 Q를 P 대신 사용할 경우 엔트로피" 는 확률변수 P와 Q의 cross entropy, 즉 H(p, q)이다.
그런데 말입니다. 이쯤에서 앞서 처음에 살펴보았던 KL divergence의 위키백과 정의를 다시 살펴보자.
쿨백-라이블러 발산(KLD)은 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다.
쿨백-라이블러 발산은 어떠한 확률분포 P가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 Q를 P 대신 사용할 경우 엔트로피 변화를 의미한다.
빨간색으로 표시한 의미 부분을 잘 생각해보자.
저기서 엔트로피의 변화라고 했으므로, 저 의미가 바로 H(p, q) 에서 H(p) 를 뺀 값이 되는 것이다.
그리고 앞서 살펴본 [그림 3], [그림 4]의 수식에 의해
KL divergence, 즉 H(p, q) - H(p) 의 값은 [그림 5] 와 같이 나오는 것이다.
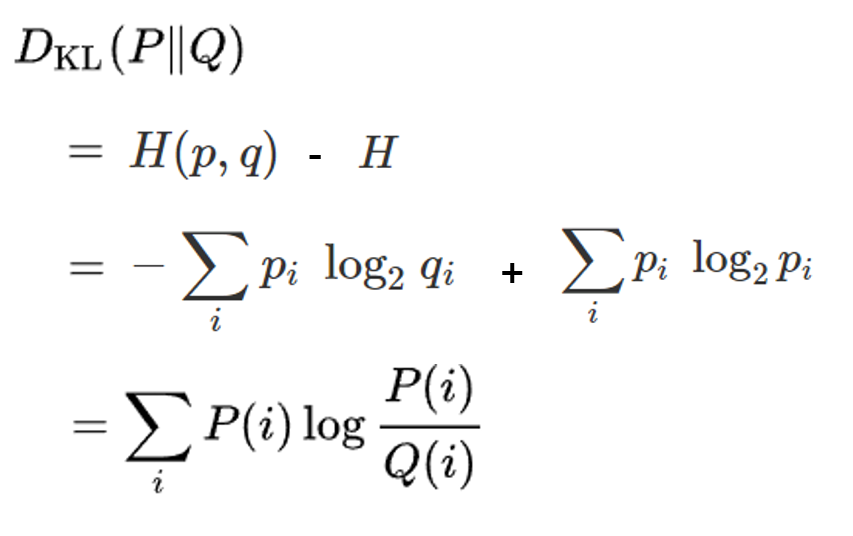
이렇게 KL divergence의 의미를 이해하고 나면, KL divergence의 두가지 대표적인 특징도 쉽게 이해할 수 있다.
1) KL divergence의 값은 0이상이다.
2) KL divergence의 값은 asymetric 하다.
우선, H(p) 값이 최소 자원량의 기댓값이므로, H(p)는 무조건 H(p, q)보다 작을 수 밖에 없다. 따라서 H(p, q) - H(p) 인 KL divergence 의 값이 항상 0 이상인 것이다.
또한, [그림 5]의 수식에서 볼 수 있듯이, p와 q의 위치가 바뀌면 KL divergence의 값 또한 바뀌게 된다. 따라서 KL divergence의 값은 symetric 하지 않고, asymetric 하다는 것을 확인할 수 있다.
(KL divergence는 distance 개념이라고 생각했던 나의 첫 생각이 틀렸음을 확인할 수 있다.)
3. JSD (Jenson-Shannon divergence)
KL divergence를 이해했다면, JSD는 정말 간단하다.
우선 M을 확률분포 p와 q의 평균이라고 했을 때, JSD는 [그림 6] 과 같이 정의할 수 있다.
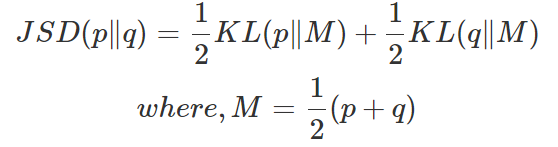
M과 P , M과 Q의 KL divergence를 각각 한번씩 구하고 이 값들을 평균 내기만 하면 된다.
M값이 P와 Q의 평균값이므로, JSD는 KLD와 다르게 symetric 하고, distance 개념으로 생각해도 되는 것이다.
오늘 내용을 정리해보면,
1. entropy는 "정보량이 생산되는 과정에서, 이를 표현하는데 필요한 최소 자원량의 기댓값" 이다.
2. cross entropy는 "어떠한 확률분포 P가 있을 때, 샘플링 과정에서 확률분포 Q를 P 대신 사용할 경우 엔트로피" 이다.
3. KL divergence는 cross entropy에서 entropy를 뺀 것이며, 확률분포 P와 Q 사이의 asymetric한 차이를 의미한다.
4. JSD는 KL divergence를 두번구해 평균을 낸 것이며, 두 확률분포 P와 Q 사이의 distance 를 의미한다.
수식 그림 출처 : https://hyunw.kim/blog
위 내용은 공부하며 정리한 것으로, 오류가 있을 수 있습니다.