[논문] Generative Adversarial Nets
논문 제목 : Generative Adversarial Nets
0. abstract
본 논문에서는 adversarial process를 통한 generative model을 estimate 하는 새로운 프레임워크, GAN을 제안한다.
GAN에서는 동시에 2개의 모델을 학습시킨다. 첫번째 모델은 데이터를 생성하는 generative model G 이고, 두번째 모델은 데이터의 진위여부를 판별하는 discriminative model D 이다.
G는 최대한 D가 실수를 하도록 하는 것, 즉 G가 만든 데이터와 실제 데이터를 D가 판별 못하도록 하는 것이 목적이다.
G와 D 모델이 multilayer perceptron 구조를 가지고 있다면, backpropagation을 통해 학습이 가능하다.
GAN을 이용하면 별다른 추가적인 조치 없이 G와 D를 양질의 모델로 학습시킬 수 있다.
1. Introduction
최근 (논문 발표 당시인 2014년도) 딥러닝 분야에서는 다양한 연구들이 진행되며 특히 데이터를 분류하는 discriminative model 에서 비약적인 성장을 나타내고 있었다.
하지만, 딥러닝 모델을 통해 데이터를 생성하는 Deep generative model 분야에서는 다양한 확률적 계산 이슈에 가로막혀 큰 성장을 하지 못하고 있는 추세이다.
본 논문에서는 이러한 문제점들을 극복한 새로운 generative model framework를 제안하였다. 해당 framework는 두개의 모델이 adversarial(적대적)으로 동작하며 학습을 진행한다.
첫번째 모델은 discriminative model 이다. discriminative model은 특정 데이터가 주어졌을 때, 해당 데이터가 진짜인지 가짜인지 classify 하는 기능을 수행한다.
두번째 모델은 generative model 이다. generative model은 데이터를 생성하는 모델로, 최대한 실제 데이터와 유사하게 만들어내는 것이 목표이다.
본 논문에서는 이 두 모델, discriminative model과 generative model을 각각 경찰과 지폐위조범에 비유하여 설명하였다. 경찰, 즉 discriminative model은 최대한 실제 돈(real data)와 가짜 돈(fake data)를 구분하도록 학습이 진행되며, 지폐위조범, 즉 generative model은 최대한 실제 돈(real data)와 비슷한 가짜 돈(fake data)를 생성하도록 학습이 진행된다.
이렇게 두개의 모델이 대립적으로 동작하며 각자의 목표에 맞춰 학습을 진행하는 모델이 바로 adversarial nets 이다.
쉽게 말해 discriminative model과 generative model은 서로의 스파링 파트너인 것이다.
2. Related work
기존의 generative model은 다양한 확률적 계산 이슈가 존재하였기 때문에 좋은 성능을 기대하기 어려웠으며, Markov chains 나, inference network와 같은 복잡한 기능들이 필요로 하다는 문제점이 존재했다.
3. Adversarial nets
본 논문에서 제안하는 Adversarial nets의 핵심 부분이다.
만약 두 모델이 모두 multilayer perceptron으로 구성되어 있다면, adversarial nets를 구성하기 쉽다.
generative model은 확률분포 Pg가 실제 data x의 확률분포를 닮도록 만드는 것이 목표이다. 이를 위해 generative model이 초기에 사용하는 noise varables z의 확률분포 Pz(z)를 정의하였다고 하자.
이 때, 본 논문에서 제안하는 adversarial network의 objective function (loss function) 은 아래 [그림 1]과 같다.

위 함수를 자세히 살펴보자.
우선 함수 V는 D와 G 2개의 변수를 가지고 있다. 하지만, G는 V 함수값을 최대한 작게 만드려하는 변수이며, D는 V 함수값을 최대한 크게 만드려는 변수이다. 즉 함수 V에 대한 G와 D의 minmax game 이라고 보면 된다.
등호의 오른쪽을 살펴보면 크게 좌변과 우변을 더하는 식으로 구성되어 있다.
좌변은 실제 data x에 대하여 log D(x) 값의 기댓값을 나타내는 식이다.
Discriminator D는 x의 값이 실제 존재하는 데이터라고 판단될 경우 1을, 가짜 데이터라고 판단될 경우 0을 반환한다. 만약 x에 실제 데이터가 들어갈 경우, D(x)는 올바르게 판단할 경우 1을 반환할 것이다. 따라서 D 의 성능이 좋을수록 좌변의 값은 증가하게 될 것이다.
우변은 가짜 data z에 대하여 log(1-D(G(z))) 값의 기댓값을 나타내는 식이다.
Generator G는 latent vector z를 입력받아 가짜 data를 생성해내는 기능을 수행한다. 이렇게 생성된 가짜 데이터는 D를 통해 진짜인지 아닌지 판단된다.
만약 Generator의 성능이 훌륭하여 D가 가짜데이터를 진짜 데이터라고 오판단 할 경우, D(G(z))의 값이 1이 될 것이며, 1-D(G(z))의 값은 0이 될 것이다.
즉 전체적으로 점검해보면, Discriminator D는 objective function의 값을 최대한 키우도록 학습을 진행할 것이고, Generator G는 objective function의 값을 최대한 작게 줄이도록 학습을 진행할 것이다.
이것이 바로 GAN의 기본적인 작동 원리이다.

위 [그림 2]를 보면, GAN 의 동작 원리를 살짝(?) 맛볼 수 있다. 아래쪽에 위치한 화살표는, Z 공간에서 뽑은 확률변수들을 X 공간에 mapping한 것을 의미한다.
(a)나 (b) 그림을 보면 알 수 있듯이, 이렇게 mapping 된 확률변수들은 실제 데이터인 검은색 점과는 다른 초록색의 확률 분포를 가지게 된다. 이렇게 될 경우, 파란색 점선으로 표현된 discriminator model의 분포 역시, 두 데이터를 명확하게 분별할 수 있는 모습을 가지게 된다.
하지만 학습 과정을 거쳐가며, Z와 X의 확률분포가 유사한 모습을 가지게 된다면, (c), (d) 그림과 같이 실제 데이터와 가짜 데이터의 확률 분포가 일치하게 학습되며, discriminator model의 분포를 보았을때 두 데이터를 분별하지 못하는 것을 확인할 수 있다.
물론 위 예시는 오직 한가지 확률 분포를 예시로 든 것으로, 수많은 확률분포들이 동시에 존재하는 실제 환경과는 거리가 있다는 점을 생각해야 한다.

위 [그림 3] 이 본 논문에서 제안하는 핵심 알고리즘이다.
우선 첫번째 for 문을 통해 epoch 수를 설정한다. 이후 두번째 for 문을 통해 k 번동안 Discriminator를 학습한다.
Discriminator를 학습하는 방법은, m개의 가짜 데이터와 m개의 실제 데이터를 뽑아 objective function에 대입하여 계산한 뒤, objective function의 함수값이 커지는 방향으로 gradient descent 과정을 거치며 학습해나간다.
k 번동안 Discriminator를 학습하는 과정이 끝나면, Generator를 학습하는 과정을 거친다.
Generator를 학습하는 방법은, m개의 가짜 데이터를 뽑아 objective function에 대입하여 계산한 뒤, objective function의 함수값이 작아지는 방향으로 gradient descent 과정을 거치며 학습해나간다. 물론 objective function의 좌변에는 z 변수가 포함되지 않으므로, 미분하는 과정에서 좌변은 사라지게 된다.
위 과정을 epoch 수만큼 반복해가며 Generator와 Discriminator를 학습하게 된고, 그 결과 Pg = Pdata의 분포를 가지게 된다.
4. Theoretical Results
4장에서는 [그림 3]과 같은 알고리즘을 통해 학습을 지속해나갔을 경우, optimal solution에 다다를 수 있는지를 증명하는 부분이다.
우선 Proposition 1을 보면, 만약 G가 fix 되어 있을 때, D는 [그림 4]와 같은 분포의 optimal 을 가지며, 이를 objective function에 대입해보면, [그림 5]와 같은 결과가 나타난다.
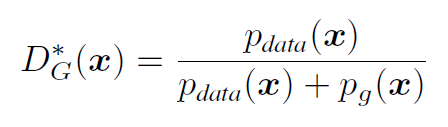
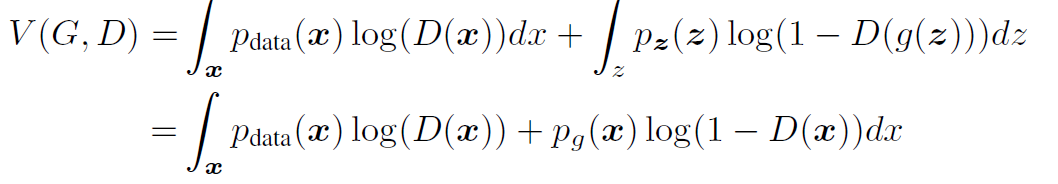
[그림 5] 의 마지막 수식을 보면, alog(y) + blog(1-y)의 꼴로 정리할 수 있으며, 이 함수의 최대값이 되는 y값은 a/a+b이기 때문에 [그림 4]와 같은 optimal D에 관한 함수값을 구할 수 있는 것이다.
이번에는 D가 optimal한 point를 가질때의 V 함수를 C(G)로 표현할 수 있으며, 이때의 식을 정리해보면, [그림 6]과 같다.
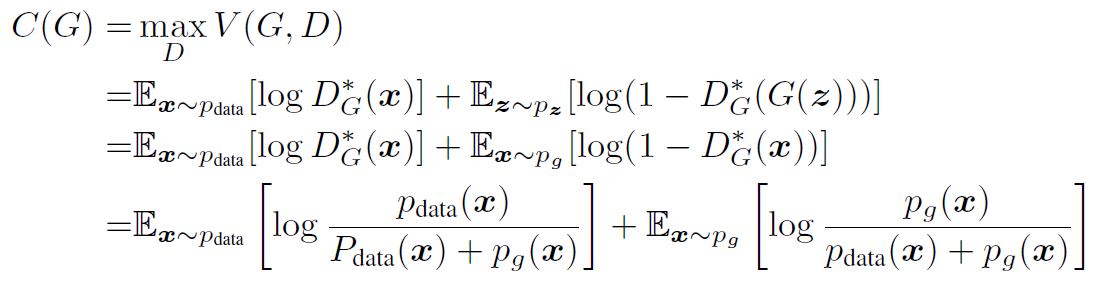
[그림 6]의 식의 최솟값이 -log 4임을 알수 있고, 이 경우는 Pdata = Pg 일 때 성립된다. 해당 기댓값 공식을 KL divergence 값으로 정리해보면 [그림 7]과 같이 나타낼 수 있으며, 이를 조작하여 하나의 JSD divergence로 나타내보면, [그림 8]과 같다.
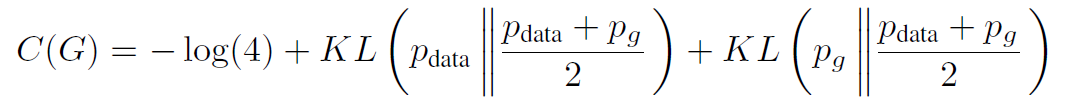

따라서 결과적으로, Pg = Pdata일 경우, global optimal에 다다를 수 있음을 보였다.
5. Experiments
실제 본 논문에서 제안된 GAN 모델을 사용해 generate model를 수행한 결과 [그림 9]와 같이 MNIST / Toronto Face Database에 적용했을 경우, 다른 generate model에 비해 높은 성능을 보이는 것을 확인할 수 있다.
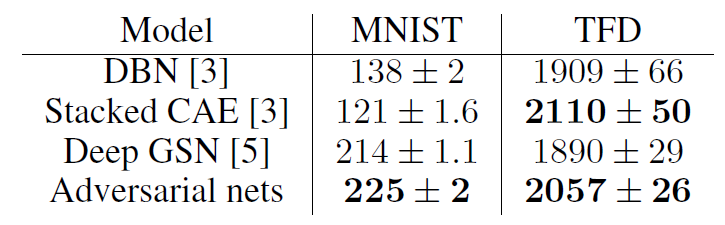
실제 GAN 모델을 통해 생성한 이미지 데이터는 [그림 10]과 같다. 오른쪽 노란색 박스들은 실제 데이터값이며, 노란색 박스 왼쪽의 데이터들은 GAN을 통해 생성한 데이터이다. 딱 봐도 알 수 있듯이, 실제 데이터와 GAN을 통해 생성된 데이터의 차이가 크지 않음을 알 수 있다.

또한, 실제 데이터와 생성된 데이터가 일치하지는 않는 것을 확인할 수 있다. 이는 GAN 네트워크가 단순히 입력 데이터를 복사해서 생성한는 것이 아니라 스스로 새로운 데이터를 생성한다는 것을 의미한다.
6. Advantages and disadvantages
우선 GAN 프레임워크의 장점은 다음과 같다.
1) 복잡한 기술 (Markov chains 등) 이 필요하지 않고 간단하다는 점
2) 다른 generative model에 비해 성능이 높다는 점
3) 데이터에 의해 generator가 직접 학습되지 않고, discriminator를 통해 간접적으로 학습되므로, 데이터의 components들이 직접적으로 복사되지 않아 다양하고 고품질의 데이터를 생성할 수 있다는 점
4) 생성된 이미지 데이터가 blurry 하지 않고 sharp 하게 표현된다는 점
또한 GAN 프레임워크의 단점은 다음과 같다
1) Pg(x)를 나타내는 explicit한 표현방법이 존재하지 않다는 점
2) D와 G는 학습하는 동안 완벽하게 synchronized 되어야 한다는 점
7. 고찰
생성 모델에 엄청난 영향을 불러온 GAN 네트워크에 관한 논문이다.
논문을 읽으면서도 '이게 된다고?' 라는 생각이 들 정도로 굉장히 신기하게 읽었던 것 같다. 구글링을 통해 간단한 GAN 프레임워크를 구현해서 MNIST 데이터셋을 이용해 돌려본 결과, 간단한 모델로도 정말 그럴듯한 데이터를 생성하는 것이 가능함을 [그림 10]과 같이 확인했다.

다만, 본 논문에서 주로 다루는 objective function의 global optimal을 증명하는 4장은 이해가 쉽게 가지 않는 부분이 많이 있었다. 특히 다양한 divergence metric이나 전체적인 증명 방식에 대해 조금 더 알아보아야 할 것 같다.
Reference
Ian Goodfellow, Jean Pouget-Abadie, et al. "Generative Adversarial Nets" Advances in neural information processing systems 27 (2014).