shine's dev log
RSA 암호화 본문
1. RSA의 탄생
RSA 암호는 Ron Rivst, Adi Shamir, Leonard 라는 세 사람이 1977년 고안해낸 암호 알고리즘이다.
비교적 최근에 만들어진 알고리즘이고 그 안전성 또한 뛰어나서 지금까지도 공개키 암/복호화 환경에서 널리 쓰이고 있다.
앞서 알아보았던 Diffie-Hellman 공개키 암호를 기반으로 만들어졌기 때문에, 방식이 꽤나 유사하다. 지금부터 RSA 암호 알고리즘에 대하여 알아보자.
2. RSA 알고리즘
1) 키생성 (개인키와 공개키 만들기) 과정
우선 다른 암호 알고리즘과 마찬가지로 키를 생성해야 한다. 공개키 방식을 사용하기 때문에 개인키와 공개키 두 개를 생성해야 한다. 공개키와 개인키는 다음과 같다.
공개키 : n과 e 두가지 정수로 이루어져 있는 키
개인키 : n과 d 두가지 정수로 이루어져 있는 키
이제 n,e,d를 어떻게 구하는지 알아보자.
n은 임의의 두 소수 p와 q를 곱하여 만들어진다.
n = p * q
다음으로 e를 살펴보면, Φ(n) = (p - 1) * (q - 1)로 구해진 Φ(n)값을 구했을 때,
e는 1 < e < Φ(n) 를 만족하는 Φ(n)와 서로소인 값이다.
참고로 Φ(n)는 n과 서로소인 1부터 n까지의 정수의 개수이다.
마지막으로 d를 살펴보면,
d는 (e * d) mod Φ(n) = 1를 만족하는 값이다.
즉, 앞서 구한 e에다가 뭐를 곱해야 n으로 나누었을 때 1이 나오는지 구하면 된다.
이제 n, d, e 값을 모두 구했다.
공개키는 (n, e)이고 개인키는 (n, d)이다.
2) 암호화 과정
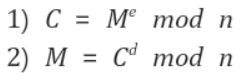
페르마 소정리에 의하면, 위의 두 식이 성립한다.
암호화 할때는 1)번 식에 공개키 (n, e)를 사용해 암호화 하고
복호화 할때는 2)번 식에 비밀키 (n, d)를 사용해 복호화 한다.
원리가 좀 어려울 뿐이지, 과정 자체는 AES나 DES보다 훨씬 간단하다.
감이 잘 안잡힐 수 있으므로, 예시를 한번 들어보자.
처음에 송신자가 임의의 두개의 소수 p = 7, q =17을 골랐다.
송신자는 p*q 를 통해 n = 119를 구했고, Φ(n) = (p-1)*(q-1) = 96이다.
1과 96 사이에 96과 서로소인 값은 5가 있으므로 e = 5가 된다.
마지막으로 5*d를 96으로 나누었을 때, 나머지가 1인 d를 구해보면 d = 77이 나온다.
이제 공개키 (n, e) = (119, 5)와 비밀키 (n, d) = (119, 77)가 생성되었다.
보내려는 메시지가 19라고 했을 때, 암/복호화를 해보면,
암호화 : 19 ^ 5 mod 119 = 66 (암호문은 66이다)
복호화 : 66 ^ 77 mod 119 = 19 (평문 19가 다시 나왔다)
3. RSA의 안정성
공격자가 공개키 (n, e)와 암호문 C를 안다면, n값을 소인수 분해하여 p,q 값을 구할 수 있고, 결국 n, d, e 값을 모두 알 수 있어서 개인키도 알아낼 수 있다.
하지만, RSA는 큰 수의 소인수 분해의 어려움을 이용하기 때문에 안전하다.
n이 충분히 크므로 p, q값을 알아내는 것이 어렵고, 이는 결국 Φ(n)를 알아내는것이 매우 어렵다. Φ(n)를 모르는 상태에서 d를 구하는 것은 매우 어려운 일이므로 RSA를 공격하기란 매우 어렵다.
현재까지는 RSA가 안전한 암호 알고리즘으로 알려져 있지만, 앞으로 컴퓨팅 파워가 증가한다면 언젠가 DES처럼 버려질 날이 올지도 모른다.
오늘 배우 내용을 정리해 보면,
1. RSA는 대칭키 암호 알고리즘으로, 큰 수의 소인수 분해의 어려움을 이용한다.
2. 암호화와 복호화는 페르마의 소정리를 활용한다.
3. RSA는 아직까지는 안전하다.
본 내용은 공부하며 작성한 것으로 오류가 있을 수 있습니다.
'보안' 카테고리의 다른 글
| 디지털 서명 & PKI (0) | 2020.08.06 |
|---|---|
| 타원 곡선 암호(Elliptic Curve Cryptography) (0) | 2020.07.30 |
| Diffie-Hellman 알고리즘 (0) | 2020.05.28 |
| 공개키 암호 (Public key Cryptography) (0) | 2020.05.27 |
| 메세지 인증 (Message Authentication) (1) | 2020.05.15 |




